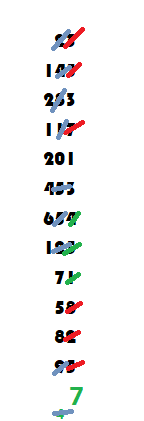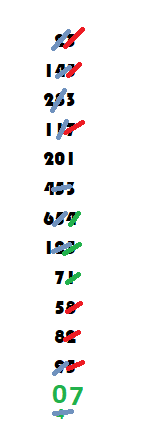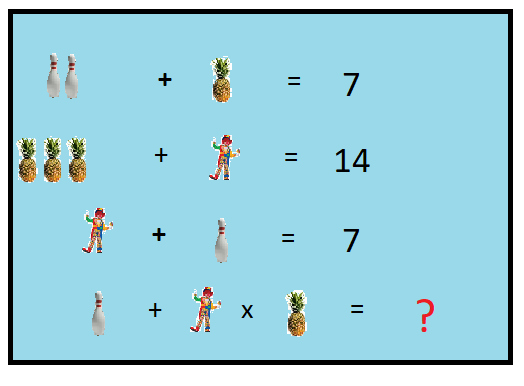Home » Archives for January 2018

Month: January 2018

Working out Recurring Decimals

A clever trick that sometimes comes up in GCSE exams is to how to turn a repeating decimal back into a fraction.

At first glance the question looks difficult… but actually it’s not really.

 

Write the decimal 0.393939393939 (recurring)  as a decimal.

 

So how do we do this?

 

Well we start with a step familiar from algebra – We use a letter!

Let r = 0.393939393939

We need to get rid of that long train of decimals – se we use the same method as when we want to lose something in solving simultaneous equations – we do a subtract

But how will that work?

Well think what 100r is

r = 0.393939393939  so 100r = 39.3939393939

[Can you see where we are going with this now?]

Now we can do a subtraction and all the numbers in the recurring chain cancel out
39.3939393939    _
0.3939393939

= 39

What we have done here is 100r – r   so this is 99r

99r = 39

So r = 39/99…  A fraction!  We’ve done it!

 

Just two more things to note

  1. We should always ‘cancel down’ fractions is we can to use the lowest numbers at top an bottom.
    So I should have finished this question by writing as  13/33.
  2. How did I know to multiply by 100? Would this work for every example?  Well, no, a careful study of what we have done shows that the key is to ‘cancel out’ all the recurring decimals. To do that, we need to ‘line up’ the same numbers in the subtraction. To do this we need to count how many numbers in the repeating pattern.. we then need that number of 0s in the ‘multiplying factor’

So if we have 0.123123123123123…   we have 3 numbers in the pattern

r = 0.123123123123123

1000r = 123.123123123123..

999r = 123

R = 123/999  = 41/333

 

Here are three more to work on,,,

 

  1. Write 0.777777777777… as a decimal
  2. Write 0.787878787878.. as a decimal

    And an advanced one…

  3. Write 0.0200200200200..  as a decimal  (That’s a bit tougher)

    Here are the answers
    0.7777 = 7/9
    0.78787878 = 78/99 = 26/33
    0.0200200200 = 20/999

Trig equation of the week….

OK  that title may be a bit misleading  – I’m not proposing a Trig problem every week…  Its also a post more aimed at A-Level students..  I’ll post on more GCSE matters later in the week

I seem to have become a member of a Q&A social networking site called Quora. Now this is very loosely edited, if it is at all, and some of the questions come with strange assumptions (e.g. How many Swedish people really wish they were Americans). The questions on Maths also cover a broad range – One asked how the questioner could find the highest Odd number under 100.

Yesterday though someone posted a question that is right in the frame that my A-level students can have a go at, so I thought I’d reproduce it here…

Rewrite  Sinx + √3Cos x  in the form A sin( x + θ) where θ > 0

OK read no further if you don’t want the answer…

Start by using the expansion of Sin(x + θ) – which by co-incidence I was teaching to a student the day I saw the question.

A sin( x + θ) = A(SinxCosθ + SinθCosx).

Now I’m going to multiply the A into the expression, and re-arrange slightly

ACosθSinX + ASinθCosx.

This is beginning to look like what we need,  but the co-efficients of Sinx and Cosx need matching.  This gives us

ACosθ = 1 (The co-efficient of Sinx)
ASinθ = √3 (The co-efficient of Cosx)

If we divide the second by the first we can eliminate A, for now

Tanθ=  √3..  so  θ = 60 Degrees

Cos60 = 1/2 so we can see from  ACosθ = 1  that A = 2.

 

And so we have the full solution

Sinx + √3Cos x  in the form 2Sin( x + 60)

Women in Maths;

The advantages of my paid work being in the afternoon is that I can listen to the radio in the morning – in bed!  This morning that meant I caught an interview I wasn’t expecting, on Radio 4’s Life Scientific, with Mathematician Eugenia Cheng..  I’ll include a link to this show here, though unfortunately you’ll need to be in the UK – and to be reading this in the next 4 weeks – for this to works (I Think).

http://www.bbc.co.uk/programmes/b09nvrcn

Please listen to the programme, its fascinating.

The first thing that moved me was her discussion of finding Maths a male world. I am slightly irritated that the first half dozen students in my ‘stable’ are all male. There was a possibility of one female student but she preferred a female tutor. I could understand that, but it worries me that parents might be seeing a need to push their son’s but not their daughters towards further achievement in Maths. This isn’t a critique of the parents currently hiring me..  I’m not sure there are any daughters in those families.

But understanding Maths is for everyone. Ones gender does not restrict you from being a real achiever in Maths.  Later blog posts will celebrate the women who have contributed.

 


Equations of Motion

For today’s post, I’m going to be looking at a subject covered in A-Level.  If that’s not your area of study, you might want to skip this – or read it and see what you learn!

There will be at least one question on an ‘Applied’  or ‘Mechanics’ exam about objects moving at constant acceleration.  There are equations to help with these questions.  One of my students remembers these as the SUVAT equations, as those are the five letters we use.

It pays to remember these for quick question answering, but its also useful and interesting to know where they come from. 

What is Acceleration?

These equations are only for situations where acceleration is constant. Velocity is how quickly distance changes – Acceleration is how quickly velocity changes. An object at rest, or moving at a steady speed are both special cases of constant acceleration – zero acceleration.  And object falling under gravity moves faster as it falls. acceleration is a constant 9.8 ms-2

from this definition comes the first equation;  u is the velocity at the start, v is the velocity at the end (in all these equations). You get the velocity at the end by adding to the velocity at the start the time multiplied by the acceleration

v = u + at

[We always talk about velocity rather than speed, because the direction can change. Velocity is like speed, but includes the direction of travel. Acceleration also has direction. It may sound strange but an object that is slowing down has acceleration  –  in the opposite direction to travel].

Area under a graph

The next equation is easier to find if you draw a graph.

Remember that in a speed Vs time graph, the area under the graph is the distance travelled.
Now we can use the formula for the area of this shape – Base x average height to get

s = t * (u + v)/2

We use s for distance in these equations

 

The other  three equations

The first two equations are derived by the definitions. There are three more that can be derived from the first two by substitution and algebraic manipulation.  With all five to hand we can choose the right one based on the information provided and required.

 

Rearrange the first equation  to make t the subject gives t = (v – u) /a

Substitute t for (v-u)/a in the second gives

s = (v+u)(v-u)/2a = (v2  – u2)/2a

We usually rearrange this so  v2  is the subject
v2  = u2 + 2as

 

The other two we find by making u and then v subject of the first equation and substituting these into the second   – These give

s = ut + at2/2

s = vt – at2/2

That’s our five equations; Look out for the post next week that gives examples on how to put these to use.

Car Parking

Quick problem of the day  – Can you tell what number space the parked car is in?  Answer added tomorrow!

 

 

 

 

 

 

(Spoiler alert- I you page down)

 

 

 

 

 

 

 

 

 

OK  – No so much an answer today, as a clue…   – From which direction are we looking at these numbers?

 

Yes  . Upside down – The answer is 87

Its all linked y’know

 When I was at school, there was some kind of assumption that students heading for A-level would be ‘Scientists’ or ‘Artists’  and it was generally assumed that I would be a ‘Scientist’…  and so I was…

But with the wisdom of age* comes the realisation that there really isn’t that much to choose between them. Maths is the language of Science  and Algebra is the language of Maths(as I say in one of the videos on this website) . Its all about communication of ideas and to limit oneself to one method is to be half the person you could be.

When teaching, particularly exam technique, I do strongly encourage students to write their answers in full sentences. Its about communicating your full idea, and it helps the person reading it (who is in a position to hand out marks!) to be more sympathetic to you.

[*I have age, I leave it to the reader to decide if I have wisdom)

In one of my favourite YouTube clips, Australian actor Tim Minchin gives the graduation address as his University. I’ll post a link below if anyone one wants to watch the whole thing, but in my favourite part of the speech, he talks about the distinction between Science and Arts…  Here are some quotes

“Please don’t make the mistake of thinking the Arts and Science are at odds with one another”

“You don’t have to be unscientific to make beautiful art”

“Science is not a body of knowledge or a belief system, Science is just a term that describes humankind’s incremental acquisition of understanding through Observation
Science* is Awesome”

“The Arts and sciences need to work together to improve how knowledge is communicated”

that includes Maths!

https://www.youtube.com/watch?v=yoEezZD71sc&t=494s

 

Adding up – Quickly!


Do you ever find yourself adding up a long list of numbers – checking a receipt maybe – and when you get to the end, you are not sure you included that 42 near the top? Or maybe you are halfway through and your dog jumps up at you, or you get a text you need to check?

Were you adding on each number at a time?
23 plus 145 , Hmm  168..  now add on 283..  that makes… Lets look at a quicker way.

 

 

We would normally add up one column at a time. But we can go further than that….

Look for sets of numbers that add up to 10. I’ve made a start here with the 7 and the 3.

 

 

Then I have collected together the two 5’s and the 8 and the 2

Sometimes its not two numbers that add up to 10. Sometimes it can be 3 numbers, like the 1, 4 and 5

Of course not all numbers can be grouped in 10s. The last three numbers here are the 3, 3 and 1 and we can add them together to make 7 with a low risk of being interrupted.

We do need to count up how many sets of 10 we had. I counted 4. That is what that small 4 is doing at the foot of the second column…. and to be included in the ‘groupings’ of course .

The second column can be added up in the same way

And here we have more left over numbers, but still easier than adding them all up!

Where is my missing £1

This is a puzzle I’ve known since I was 10, and then yesterday a friend tagged me on it on Facebook. The solution has now been added to the post.  Try answering it first before looking at the spoilers!

 

 

 

 

 

 

 

 

 

 

OK  –  Here is the answer! 

The skill in solving problems like this is noting down the information you have and trying to ignore any misdirection.  And boy, does the setter of this problem go in for misdirection!

And if you are thinking, that means bringing in skills learnt in an English comprehension class, you’d be right. School subjects may be split between Maths, English, Science, History – but in life things are never so simple. Actually I like to persuade students to write their answers in full English sentences, especially in problem solving cases.

In this situation, we have a situation involving some money, and there is money coming in (the money that each guest pays at the start) and money coming out (to the guests, the hotel and the bell boy).

Each Guest pays £10. That’s £30 ‘in the system’

But who has this money at the end?  The hotel has £25. The bell boy keeps £2. Each of the guests has £1 return to them by the bell boy. That is a total of £30 (£25 + £2 + £1 + £1 + £1)

Or if you prefer lets look and gains and losses. The guests have spent £9 each, making £27.   £25 goes to the hotel, £2 to the bell boy. A total of £27. Gains = Losses. Just as we’d expect.

 

 

 

 

 

So lets remind ourselves of the question. This asked us to add the £9s that the guests paid in and £2 the bell boy kept.  But these numbers are from different parts of the question! (As highlighted in grey and blue)   There is really no reason why they should be added. The fact that the total came close to £30 was a coincidence (or not, since the questioner chose the numbers to confuse!)

So in summary, ignore the last paragraph until you have come to your own understanding about the ins and outs. And then you won’t fall into the trap of adding an ‘in’ amount to an ‘out’ amount.

 

Clowning About (The answer)

Lets work through to the answer.

The first thing to do is simplify the situation by taking the clown out of the picture.  We know the clown + the pin is worth 7…
so clown = 7 – pin.

Now we replace the clown in the 2nd equation with ‘7 – Pin’

From the first equation  the pineapple = 7 – 2 pins

We can change the 2nd equation to be just about Pins.

3 x ( 7 – 2 Pins) + 7 – Pin = 14

28 -7 Pins = 14

so 7 Pins are worth 14, and 1 pin is worth 2. We can find from the other two equations.

I’ve solved this by a ‘substitution method’ I could also have done this by adding or subtracting equations.  But the key is to eliminate some of the variables until we have one, then substitute back.

 

 

The final stage relies on knowing we should do the multiplication first, so the answer is

2 + 5 x 3 = 17.

 

Clowning about

I know getting the better of equations is one of the skills that can take more work if you are not a natural at Maths.

That’s why I’ve been fascinated with how this has become a craze on Social Media.  Give someone a picture with bottles of beers and balloons and it becomes a problem worth solving.

Here is one of my own –  OK, I’ve gone with clowns, Pineapples and bowling pins. Can you work out what the ? is worth?

Clues –

1 –  Try to eliminate the clown from your enquiries
2- This should help you find the value of the Pineapple, then bowling pin, and then clown.
3, Remember the BODMAS rule – This is the mistake people most often make.

(pssst  – The solution will be posted in three days)