For today’s post, I’m going to be looking at a subject covered in A-Level. If that’s not your area of study, you might want to skip this – or read it and see what you learn!
There will be at least one question on an ‘Applied’ or ‘Mechanics’ exam about objects moving at constant acceleration. There are equations to help with these questions. One of my students remembers these as the SUVAT equations, as those are the five letters we use.
It pays to remember these for quick question answering, but its also useful and interesting to know where they come from.
What is Acceleration?
These equations are only for situations where acceleration is constant. Velocity is how quickly distance changes – Acceleration is how quickly velocity changes. An object at rest, or moving at a steady speed are both special cases of constant acceleration – zero acceleration. And object falling under gravity moves faster as it falls. acceleration is a constant 9.8 ms-2
from this definition comes the first equation; u is the velocity at the start, v is the velocity at the end (in all these equations). You get the velocity at the end by adding to the velocity at the start the time multiplied by the acceleration
v = u + at
[We always talk about velocity rather than speed, because the direction can change. Velocity is like speed, but includes the direction of travel. Acceleration also has direction. It may sound strange but an object that is slowing down has acceleration – in the opposite direction to travel].
Area under a graph
The next equation is easier to find if you draw a graph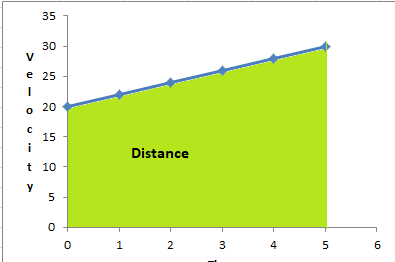 .
.
Remember that in a speed Vs time graph, the area under the graph is the distance travelled.
Now we can use the formula for the area of this shape – Base x average height to get
s = t * (u + v)/2
We use s for distance in these equations
The other three equations
The first two equations are derived by the definitions. There are three more that can be derived from the first two by substitution and algebraic manipulation. With all five to hand we can choose the right one based on the information provided and required.
Rearrange the first equation to make t the subject gives t = (v – u) /a
Substitute t for (v-u)/a in the second gives
s = (v+u)(v-u)/2a = (v2 – u2)/2a
We usually rearrange this so v2 is the subject
v2 = u2 + 2as
The other two we find by making u and then v subject of the first equation and substituting these into the second – These give
s = ut + at2/2
s = vt – at2/2
That’s our five equations; Look out for the post next week that gives examples on how to put these to use.