In yesterday’s post I considered how we can find the area of a many sided regular polygon. Today we will look at taking our Polygon formula to the limit.
Yesterday’s formula
So, given the number of sides and the length of each one. We found the formula
Now let’s consider the Circumference
For this post I’m going to add Circumference into the mix. We know that word for circles but we can use it for polygons too – its just another word for perimeter – the distance all the way round the shape, the length L, S times
C = L x S
In the formula, we are now going to replace the L with a C, since the more sides we have, L is going to get small, and C is an easier thing to measure.
L = C/S is just a rearrangement of the formula above which we can use to replace L in our area formula
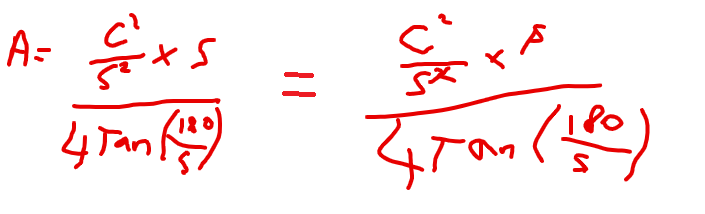
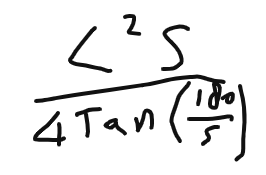
This gives a formula with C in of
A = C2/4STan(180/S)
We now have moved all mention of S to the bottom of our formula.
Now if C is kept the same but S gets bigger and bigger, what does that mean for our formula?
As S gets bigger. 180/S will get closer to 0, and so too will Tan(180/S), S will obviously get bigger, so what does that mean for S x Tan(180/S).
What happens when S gets very big?
Now this is where I am going to cheat a little; It may be possible using mathematical techniques to see what happens as S gets bigger, but I am just going to plug some numbers in
| S | S x Tan(180/S) |
|---|---|
| 10 | 3.249 |
| 50 | 3.146 |
| 100 | 3.143 |
| 1000 | 3.142 |
This shows that S has to get quite big before the pattern is clear, but it seems that
S x Tan(180/S) is getting close to a very familiar number, π.
So it seems for very large values of S
A = C2/4π
Remember that C = 2πr2 so C2 = 4π2r2
So, A = 4π2r2/4π
The 4π on the bottom cancels with elements on the top and we are left with
A = πr2
Which is the familiar area of a circle, and if you think about polygons with many, many sides you will see they are very close to being circles. That’s what we get by taking our our Polygon formula to the limit.
This is why I love maths! Everything fits together!

 This one comes from the Independent’s Website and the story that goes with it says its for a 7 year old, I’d be interested to see a seven year old tackle it – I have no doubt that a bright one could! I’m going to share it will my year 10 (15 year old) student this afternoon, and I’ll report back tomorrow, with an answer!
This one comes from the Independent’s Website and the story that goes with it says its for a 7 year old, I’d be interested to see a seven year old tackle it – I have no doubt that a bright one could! I’m going to share it will my year 10 (15 year old) student this afternoon, and I’ll report back tomorrow, with an answer!