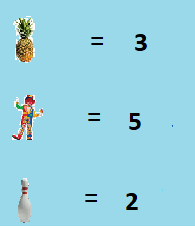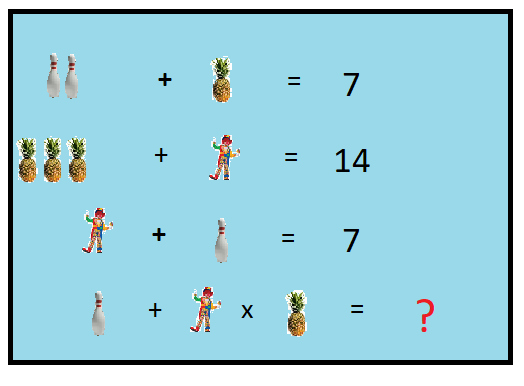I thought I’d finish the week with a problem from my friends at ‘Quora’.. but then I found most of this weeks problems were difficult questions requiring University Maths! Yes I could follow (most) of it but it was all a little ‘off-piste’ for this diary, So here is a problem with can solve using Simultaneous equations

A word problem

So I have picked out a wordy problem that might look complicated at first sight, but we really just need to turn it into a couple of equations…  Let’s see

 

 

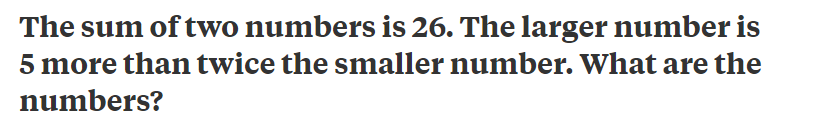
Lets call our numbers a and b – That’s always a good start with Algebra.

 

Let’s get some simultaneous equations

The first equation gives us the sum. So

a + b = 26.

With the second equation, we need to decide which is the larger number. It doesn’t matter which be choose. Let’s say a is larger.

a =  5 + 2b  (a has a value 5 more than twice b)

This is where we can solve the simultaneous equations. I’ll make a video on all the ways to do this soon, but for now I am going to solve these ‘by substitution’

I am going to substitute into the first equation the expression for a in the second. In the () you will see I have replaced ‘a’ with what a = in the second

(5 + 2b) + b = 26

We can together together terms

5 + 3b = 26

Take 5 from both sides

3b = 21

And from this see that b = 7. And so a = 19 (Twice b plus 5).

Check your answer with the other equation

As a final check 7 + 19 = 26

So there we have it the two numbers are 19 and 7

For more information on solving simultaneous equations, take a look at this More Help on simultaneous equations

 

This is a question I asked myself when I returned to tutoring Maths a few years ago. Number machines often turn up in questions of Foundation papers. They provide a useful introduction to quite a few things

• Algebra
• Functions
• Computer Programming – Which is what I was doing before I turned to Tutoring.

 

Here is an example Number Machine. The idea is we ‘feed in’ a number on the left, and see what comes out on the right.

A simple starter question would be : If a 4 in entered into this number machine, what would the result be. Number machines work left to right, just like reading. In this case, if the input is 4, we follow the boxes left to right and get  4 x 4 = 12 then + 2 = 14 .

A more advanced question would be – If the output is 8, what is the input.  This asks us to move right to left but also do the operations if reverse. Remember reverse of adding is taking away. The opposite of multiplying is dividing.

8 – reverse of + 2 is -2   so the number between the boxes is 6.  6 Divide by 3 is 2.  So the in number must be 2.

Try putting 2 into the machine and see how this is a reverse of what we did above.

The more complicated questions miss out the instructions. For example.

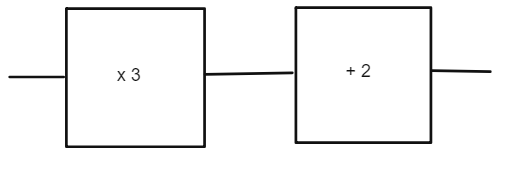
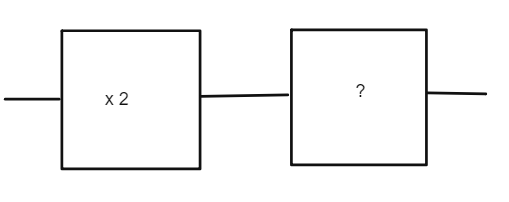If we put 6 into this number machine we get 6 out. What is missing in the second box?

Clue – Its an subtraction sum.

I’ll show how to answer that in my next post.

 

Today’s post is on a GCSE subject, but quite an advanced one…  Solving Simultaneous  equations by substitution

I say advanced; I think its not often covered, but I think it can be followed;  There might just be some exciting algebra to do

 

Lets start with a refresher on how to solve simultaneous equations

To solve these equations

4x + y =  9
3x – y =  5

we know we need to add the equations together, to get rid of the y.

Sometimes we have to be a bit cleverer, and multiply one of the equations by something. For example

4x + y =  9
3x –2y =  4.

We have to multiply the first equation by 2 so the number in front of the y is the same. Otherwise the y won’t disappear when we add.

This is called ‘solving by addition/subtraction’

It only works sometimes. This new method words more often. It’s called ‘solving by substitution’

 

Solving By Substitution

Did you solve the first equations? You should have got x = 2 and y = 1

Now let’s change the first equation so its y = something. We can -4x from both sides.  This gives us

y = 9 – 4x.

Now, this is where the ‘substitution’ comes in.  We change the y in the other equation –

3x – (9-4x) = 5

We re-arrange this, remembering that – -4x = + 4x!
3x – 9 +4x = 5
7x = 14; x = 2..  and y = 1

Now that looks similar but more complicated. In fact I would recommend solving this equation the way we knew before.

So why am I showing you ‘substitution’?

To show the result is the same, and to get ready for when the other method doesn’t work.

 

For example
2x²  + y²  =11
y – x = 2

Here we have ‘squared’ in the mix, and this makes it hard to see how we can get rid of terms by adding or subtracting to two equations. This is where substitution comes into its own

Change the 2^nd equation to say y = x + 2 (I’ve just added the x to both sides)
Substitution y = x + 2 into the first

2x² + (x + 2)² = 11

We have to a little work here, multiplying the brackets out and rearranging the terms
2x² + x² + 4x + 4 = 11
3x² + 4x – 7 = 0  (I’ve combined the x² terms and taken 11 from both sides)
Factorising this gives
(3x  + 7 ) (x  – 1)

That could be quite a hard factorisation to see straight off, though it helps that not many pairs of numbers multiply together to make -7. A little ‘trial and error’ may help.
So x = 1 or x = -7/3

Now remember y = x + 2 so

When  x = 1, y = 3..  That’s quite easy to see

When x = -7/3, y = -1/3. Just add on 2;

 

Lets work through to the answer.

The first thing to do is simplify the situation by taking the clown out of the picture.  We know the clown + the pin is worth 7…
so clown = 7 – pin.

Now we replace the clown in the 2nd equation with ‘7 – Pin’

From the first equation  the pineapple = 7 – 2 pins

We can change the 2nd equation to be just about Pins.

3 x ( 7 – 2 Pins) + 7 – Pin = 14

28 -7 Pins = 14

so 7 Pins are worth 14, and 1 pin is worth 2. We can find from the other two equations.

I’ve solved this by a ‘substitution method’ I could also have done this by adding or subtracting equations.  But the key is to eliminate some of the variables until we have one, then substitute back.

 

 

The final stage relies on knowing we should do the multiplication first, so the answer is

2 + 5 x 3 = 17.

 

I know getting the better of equations is one of the skills that can take more work if you are not a natural at Maths.

That’s why I’ve been fascinated with how this has become a craze on Social Media.  Give someone a picture with bottles of beers and balloons and it becomes a problem worth solving.

Here is one of my own –  OK, I’ve gone with clowns, Pineapples and bowling pins. Can you work out what the ? is worth?

Clues –

1 –  Try to eliminate the clown from your enquiries
2- This should help you find the value of the Pineapple, then bowling pin, and then clown.
3, Remember the BODMAS rule – This is the mistake people most often make.

(pssst  – The solution will be posted in three days)