A problem question I tackled with a student yesterday asked..
What is the smallest number that has 1, 2, 3, 4, 5, 6, 7, 8 and 9 as a factor
I had just taken along a pack of ‘challenging questions’ because he is an able student but needs a challenge. As is happens, this is a question about Lowest Common Multiple, and I had been looking at this a day earlier with another student.
Anyway, yesterday’s student was quick to point out that we can ignore 1 because ‘1 goes into everything’. That was a good start!
He then started listing all the numbers 9 goes into – the 9 times table – and checking off each number against 8, 7, 6 and so on… When I showed him the quicker way I’m sharing below here, he admitted ‘That would have taken a long time”
The quicker method is to split all the numbers into their prime factors
2 = 2; 3 = 3; 5 = 5; 7 = 7 – thats the prime numbers in the list
4 = 2 x 2; 6 = 2 x 3; 8 = 2 x 2 x 2; 9 = 3 x 3
Now, consider the answer we are going to get. As I usually do I’ll give this a letter, but for a change I’ll call it Z!
Z is just a number, even if we don’t know what it is yet. so we will be able to write Z as prime factors, and, those Prime factors are going to be a bit like the prime factors we’ve already found for all the numbers.
We could find Z by combining all the prime factor lists we have, but we will find we don’t need ALL of them.
For example 8 = 2 x 2 x 2 – and we find we don’t also need to add in the 2s from the 4 and the 6! With the 2s in the 8, we have them covered.
Taking that for all the numbers, for each prime number in our list, we only need as many as covers the most in any number.
2 x 2 x 2 – because 8 is the number with the most 2s
3 x 3 – because 2 is the most number of 3s in the prime factors of our numbers
then 5 and 7, because they only appear once in any list
The answer is – 2 x 2 x 2 x 3 x 3 x 5 x 7. You can do this on your calculator and get 2520 – The answer to this question)
[Actually, I try not to use a calculator unless I have to; keeps my mind sharp! Instead I pick numbers from the list that make multiplying in stages easier.
Pick the 2 x 5 = 10. The 7 x 3 x 3 = 63 – Gives 630. Then double this twice for the other 2 2s – 1260 then 2520!]
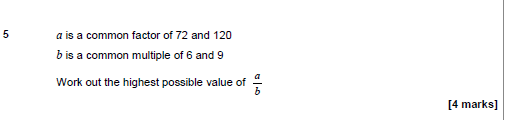
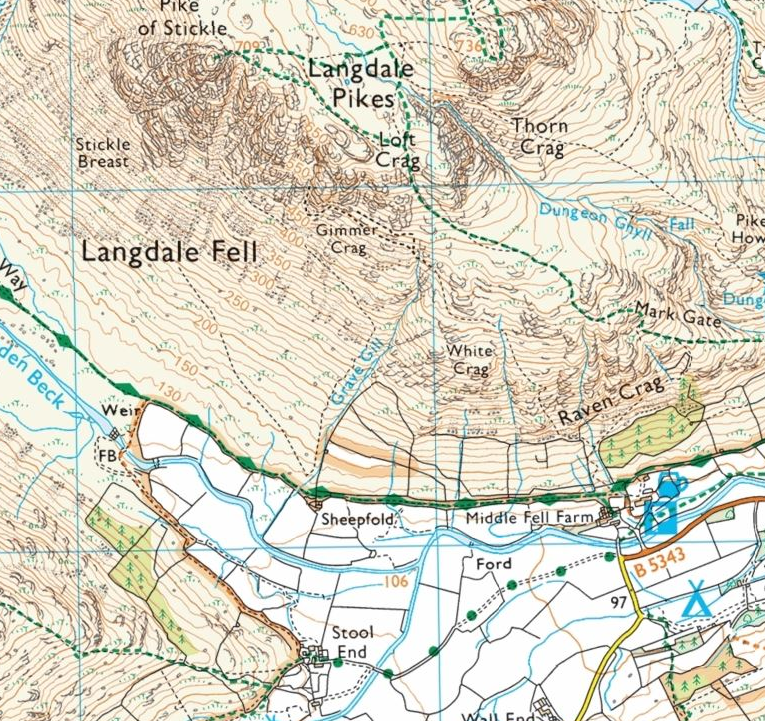 Now here is a map of one of my favourite places in the world – and comments from anyone who agrees are welcome! The point is, a map represents the place you want to visit so obviously has to be a lot smaller than the place itself! (Ok so this reminds me of a favourite Blackadder joke but lets not get off the point)
Now here is a map of one of my favourite places in the world – and comments from anyone who agrees are welcome! The point is, a map represents the place you want to visit so obviously has to be a lot smaller than the place itself! (Ok so this reminds me of a favourite Blackadder joke but lets not get off the point)
 This one comes from the Independent’s Website and the story that goes with it says its for a 7 year old, I’d be interested to see a seven year old tackle it – I have no doubt that a bright one could! I’m going to share it will my year 10 (15 year old) student this afternoon, and I’ll report back tomorrow, with an answer!
This one comes from the Independent’s Website and the story that goes with it says its for a 7 year old, I’d be interested to see a seven year old tackle it – I have no doubt that a bright one could! I’m going to share it will my year 10 (15 year old) student this afternoon, and I’ll report back tomorrow, with an answer!