In the last post I showed the difference between a Continuous curve and a Discontinuous curve, with a few examples from well known curves.
In this post I am going to show that this can be useful to know in answering a certain sort of question.
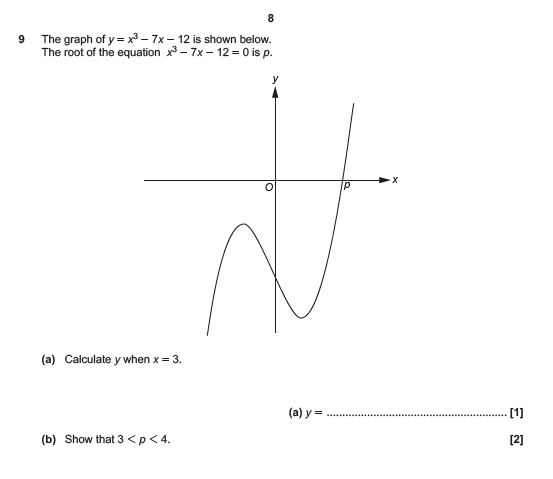
I’m not going to do this whole exam question.
The first part involves putting the value x = 3 into the given equation. You will get the answer y = -6
Use the value x = 4 and you get the value y = 20.
This is where the fact that this is a continuous line is so important. You know that the line must cross the line y = 0 somewhere between x=3 and x=4 , and that is what we mean by the root.
If you don’t believe that, think of the equation y=1/x.
If x = -2, the y = -1/2
If x = 1 then y = 1.
The same situation; y goes from negative to positive. Does that mean we have a value of x between -2 and 1 for which 1/x = 0?
No it doesn’t, because the curve for y=1/x is not continuous. we can only use that rule for continuous curves.
Note: Some curves, such as y=1/x in fact, are continuous for much of their length. There is just one place where it is not. So you can use the rule above if the curve is continuous in the RANGE of numbers you are working in.