For today’s question I am looking at one in Linear algebra
I should start by saying what I mean by ‘Linear Algebra’, which is a term I sometimes use with GCSE students and find they haven’t heard of it… I guess that’s just me using language from ‘further along’ the Maths road, that will become second nature to you later on if you continue with the subject…… anyway it means what it sounds like.. algebra as its used to describe lines.
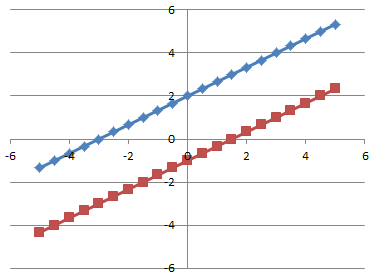
Anyway, on with the question – there is not a lot of work to do here, but to get to the answer you need to remember how we can get to two lines being parallel through their equations – and the secret lies in their gradients. Two lines will be parallel if their gradients are the same. on the graph below I show two lines, one with the equation y = 2/3 x + 2 and one with the equation y = 2/3 x – 1. As you can see on the graph, the lines are parallel. The equations are in the familiar form y = mx + c so we read off the gradients as the same, 2/3 in each case.
In the question we have from the exam, that is not so. Well, not for both. We can see the gradient from the first line – that is 3.
Some re-arrangement is needed, and that’s the small amount of work needed.
3y – 9x + 5 = 0 – Add 9x and take 5 from each side gives
3y = 9x – 5 – Divide throughout by 3
y – 3x – 5/3. We don’t really need the 5/3 part; we can see though from the 3x that the lines have the same gradient so are parallel.
Proved as required.