Well, its hot here in the UK, and that may not make people think immediately of maths! But its a subject useful for every occasion. Today we look at the Maths of Temperature

So today I am writing about ‘temperature’ and

how it helps us understand Maths.

Temperature is the sample I often use when explaining negative numbers to students.  It is one example were minus numbers are used in everyday life – but perhaps not in this weather!

 

Formulas used in temperature

After negative numbers, another interesting and useful part of the Maths of Temperature is using conversion formulas and rearranging formulas.

There are two temperature scales in common use; Celsius and Fahrenheit, both named after the scientist who invented them.

(We use abbreviations  ͦ C  and  ͦ F for these.  Some people think the first of these is called Centigrade. This is understandable because we started using  ͦ C in the UK about the same time we started using metric measurements like centimetres. But it’s more accurate to use the inventor’s name. The initial is just co-incidence)

We define both scales by the freezing and boiling points of water – 0 and 100 in Celsius; 32 and 212 in Fahrenheit. Quite why we use these numbers for Fahrenheit seems very strange, but its likely that wasn’t how Mr Fahrenheit came up with his scale.

We can use these numbers to find the formula to convert  ͦ C  to  ͦ F

Let’s say this formula is F(c) = ac + b – It is a linear function, we do know that

F(0) = a x 0 + b = 32 so b = 32

F(100) = a x 100 + 32 = 212

From this we can get 100a = 180  (I’ve simplified the a and taken 32 from both sides

This gives a = 9/5  (180/100 simplified)

So F = 9C/5 + 32 – which is the familiar formula.

Rearranging a formula.

That is useful for temperature in Fahrenheit if we know the temperature in Celsius.

If we know the temperature in Fahrenheit but we would like to know it in Celsius, then we need to rearrange the formula. This is especially useful if we need to do this calculation several times.

F = 9/5 * C – 32

F + 32 = C * 9/5

C = (F – 32) * 5/9

This is a subject on which I helped a student once after his Science tutor said he wasn’t getting it. After working on it with me, the Science teacher noted the improvement.

In fact a study of rearranging a formula is not only useful in Maths. It is also useful in the study of the Sciences, especially Physics

This has been a short post, tidying up the last one.

In today’s post I’ll be investing further the area of a Polygon. Is there a formula for the area of a regular Polygon!

What are the familiar Polygons?

If it is 3 sided or 4 sided – a triangle and a square – then we know the formula for area, but I was thinking – what about a formula that works for any regular polygon – That is to say, one with all the sides the same.

 

 

 

 

Here is a polygon and lets say the length of all the sides is L.  You can count the sides here and see there are 8 – this is an octagon  – but let this represent ‘any polygon’ with a number of sides S.

Read more about polygons and their angles here.

Area of a polygon : More general approach

I will be looking for is a formula where A = something with L and S in, as they are the two ‘properties’ of the polygon that might change in our ‘general’ polygon

The art of finding the area of any unfamiliar shape is to divide it into shapes for which you know how to find the area.  Any polygon can be divided into triangles by drawing lives from each corner into the middle.

How many triangles?  S  – One for each side of the polygon.

 

What is the area of each of these triangles?  For this we need to know the base and the height; The base is L. To find the height we will need to use some trigonometry. Half of the triangle is a right angled triangle. I am going to use the angle at the top of the half triangle, which I have labelled x

The full angle at the top is 1/S of the 360 degrees at the centre  =

360/S.   x is 1/2 of this  = 180/S

Tan(x) = L/2  /  h  (Opposite/Adjacent where the ‘opposite’ is half the base  and h is what we will call the height, for now.

Add in some detail and rearrange

Tan(180/S) = L/2h
Rearrange again to give h = L/2Tan(180/S).

Area of the small triangle is (using 1/2 x b x h)   = L²/4Tan(180/S).

This is only 1 triangle out of S triangles, so the formula for the whole polygon is

Checking my formula with some examples

Now, as I said at the start, I worked out this formula a week ago, bit I wanted to check my work because it looked a bit cumbersome….. But it does seem to stand up, and I’ll show you how.

There are two polygons for which we know another formula; The Triangle and the square (S = 3 and S = 4).  Lets see what happens if we make S= 4

A =  L² x 4 / 4Tan(180/4)

Tan(180/4) = Tan(45) = 1 – so we can leave this term out. Also the 4 and 4 can cancel, and we get

A =  L² – the simple and familiar formula for the area of a square!

Checking this for the triangle is more tricky because we to find the ‘normal’ area for a regular 3-polygon – or as we usually call it, an equilateral triangle.  For this we need our old friend, Pythagoras’ Theorem.

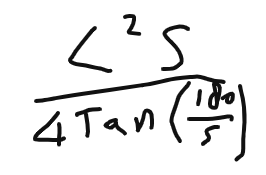
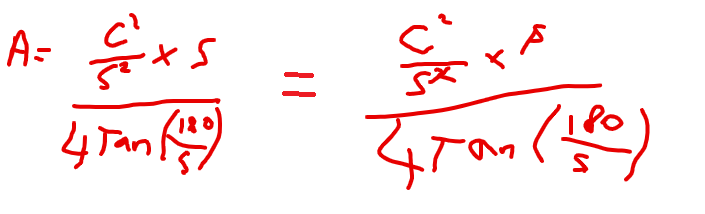
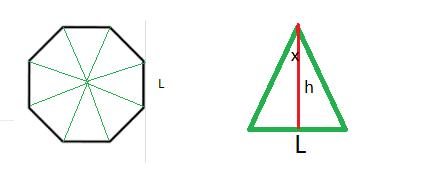
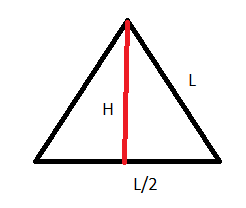Using the theorem in half the triangle, we get

(L/2)² + H² = L²

H² =  L² – L²/4  = 3L²/4

H = √3L/2

so A = √3L²/4

Now lets see what we get from our polygon formula with S=3.

Tan(180/3) = Tan 60 = √3

A = (L² x 3)/(4 x √3)

Remember that 3/√3 = √3

so A = √3L²/4

The same as with the direct method!

Conclusion

That, I claim, justifies my formula.  If anyone can think of an alternative way of finding the area of a pentagon or hexagon, then the formula can be checked for these shapes too.

Now, interesting things happen to our formula if S gets bigger and bigger, but that will have to wait for another post!

In yesterday’s post I wrote about how we can find the internal angle in regular polygons, and how the total of all the internal angles have the pattern 180, 360, 540, 720.   This patterns isn’t too hard to remember, but the pattern is even easier for the external angle.

What is an external angle?

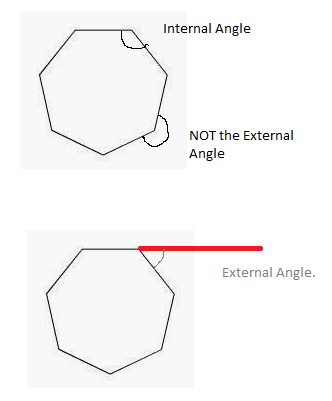Actually its easier to understand what is going on if we look at the external angles.

It’s important to know what the external angle is.  It is NOT the angle all the way round the outside

It is the angle between each line.. if it were drawn longer..  and the nest line round the shape in that direction.

It is useful to imagine you are walking around the shape. The external angle is the angle you  turn your body round at each corner.  Then once you have walked round the whole shape..  and ready to start again ..  you have turned the full 360°

So the size of each external angle = 360°/Number of angles.

The number of angles is the same as the number of sides, of course.

For more information on external angles, look here

Comparing the Angle Formulas

 

That is an easier formula than the one we saw for the internal angles, but I always get curious in these situations. We have two formulas…  do they work together?

For a given regular polygon lets say it has S sides (so also S corners, A internal angles and S external angles). Let A be the size* of each internal angle and X be the size* of each external angle.

*They will all be the same because this is a regular polygon. This sudden move into the language of algebra is because we don’t know how many sides our polygon has – we are looking at all polygons at the same time.

X = 360/S (Today’s formula)
A = (S-2) x 180/S (Yesterday’s formula for the size of each angle)

Also, X = 180 – A : The two angles make a straight line. Look at the diagram.

To show these formulas all say the same thing, we need to combine two of them and show we get the other one. This can be done a number of ways, but I’ll only show one here.

Take X = 180 – A  and substitute in the formula for A

X = 180 –  180(S-2)/S

X = (180S – 180(S-2))/S – I’ve made the whole equation ‘over S’ by including the first 180 in the fraction)

X = (180S – 180S + 360)/S  I’ve multiplied out the bracket on the top

X = 360/S – Because 180S – 180S = 0!
And so we get to the other formula for X

Interesting patterns can be found if we look at the sizes of the angles in polygons. I am referring specifically to regular polygons.

What makes a Polygon regular?

A regular polygon is any shape where all the sides are

the same length. Some of these shapes we might not immediately recognise as a ‘regular polygon’ because we have another name for the shape – Square and Triangle – specifically an ‘equilateral triangle’

 

In this post we are going to look at how big each angle is in each shape.

 

What do we know about angles in Polygons?

We know that angles in a triangle add up to 180° – That is something we learn – and that a square is made up of four right angles – 4 x 90° = 360°

The next polygons are the pentagon, hexagon,  heptagon and octagon. And so with these we can continue our research into the angles in Polygons

The hexagon is probably the most familiar of these words, the pentagon is perhaps most famous for the US department of defence. The other two words might be new to you (though where I was at university the Octagon was the main conference building – it was where I graduated!)

The sums of the angles in these shapes are 540°, 720°, 900° and 1080°.

You might see a pattern there – each number goes up by 180°.

We can turn this into a formula where S is the number of sides of the polygon

Total of Angles = (S – 2 ) x 180.

From this we can work out the size of each angle in a regular polygon. Because the sides are equal, so are all the angles.

Each angle is 180(S-2)/S.

In this post I have been looking at the ‘Internal Angles’.  Actually, its easier to show that these formulas work if we consider the external angles.  What are they, you might wonder?

Well that will be the subject of the next post!