In yesterday’s post I wrote about how we can find the internal angle in regular polygons, and how the total of all the internal angles have the pattern 180, 360, 540, 720.   This patterns isn’t too hard to remember, but the pattern is even easier for the external angle.

What is an external angle?

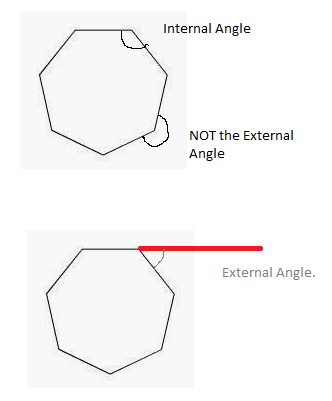Actually its easier to understand what is going on if we look at the external angles.

It’s important to know what the external angle is.  It is NOT the angle all the way round the outside

It is the angle between each line.. if it were drawn longer..  and the nest line round the shape in that direction.

It is useful to imagine you are walking around the shape. The external angle is the angle you  turn your body round at each corner.  Then once you have walked round the whole shape..  and ready to start again ..  you have turned the full 360°

So the size of each external angle = 360°/Number of angles.

The number of angles is the same as the number of sides, of course.

For more information on external angles, look here

Comparing the Angle Formulas

 

That is an easier formula than the one we saw for the internal angles, but I always get curious in these situations. We have two formulas…  do they work together?

For a given regular polygon lets say it has S sides (so also S corners, A internal angles and S external angles). Let A be the size* of each internal angle and X be the size* of each external angle.

*They will all be the same because this is a regular polygon. This sudden move into the language of algebra is because we don’t know how many sides our polygon has – we are looking at all polygons at the same time.

X = 360/S (Today’s formula)
A = (S-2) x 180/S (Yesterday’s formula for the size of each angle)

Also, X = 180 – A : The two angles make a straight line. Look at the diagram.

To show these formulas all say the same thing, we need to combine two of them and show we get the other one. This can be done a number of ways, but I’ll only show one here.

Take X = 180 – A  and substitute in the formula for A

X = 180 –  180(S-2)/S

X = (180S – 180(S-2))/S – I’ve made the whole equation ‘over S’ by including the first 180 in the fraction)

X = (180S – 180S + 360)/S  I’ve multiplied out the bracket on the top

X = 360/S – Because 180S – 180S = 0!
And so we get to the other formula for X