In today’s post I’ll be investing further the area of a Polygon. Is there a formula for the area of a regular Polygon!

What are the familiar Polygons?

If it is 3 sided or 4 sided – a triangle and a square – then we know the formula for area, but I was thinking – what about a formula that works for any regular polygon – That is to say, one with all the sides the same.

 

 

 

 

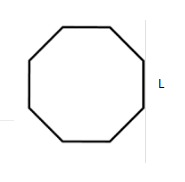
Here is a polygon and lets say the length of all the sides is L.  You can count the sides here and see there are 8 – this is an octagon  – but let this represent ‘any polygon’ with a number of sides S.

Read more about polygons and their angles here.

Area of a polygon : More general approach

I will be looking for is a formula where A = something with L and S in, as they are the two ‘properties’ of the polygon that might change in our ‘general’ polygon

The art of finding the area of any unfamiliar shape is to divide it into shapes for which you know how to find the area.  Any polygon can be divided into triangles by drawing lives from each corner into the middle.

How many triangles?  S  – One for each side of the polygon.

 

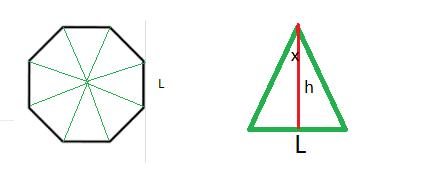
What is the area of each of these triangles?  For this we need to know the base and the height; The base is L. To find the height we will need to use some trigonometry. Half of the triangle is a right angled triangle. I am going to use the angle at the top of the half triangle, which I have labelled x

The full angle at the top is 1/S of the 360 degrees at the centre  =

360/S.   x is 1/2 of this  = 180/S

Tan(x) = L/2  /  h  (Opposite/Adjacent where the ‘opposite’ is half the base  and h is what we will call the height, for now.

Add in some detail and rearrange

Tan(180/S) = L/2h
Rearrange again to give h = L/2Tan(180/S).

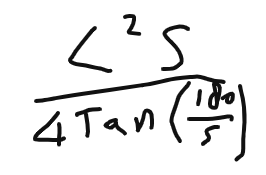
Area of the small triangle is (using 1/2 x b x h)   = L²/4Tan(180/S).

This is only 1 triangle out of S triangles, so the formula for the whole polygon is

Checking my formula with some examples

Now, as I said at the start, I worked out this formula a week ago, bit I wanted to check my work because it looked a bit cumbersome….. But it does seem to stand up, and I’ll show you how.

There are two polygons for which we know another formula; The Triangle and the square (S = 3 and S = 4).  Lets see what happens if we make S= 4

A =  L² x 4 / 4Tan(180/4)

Tan(180/4) = Tan(45) = 1 – so we can leave this term out. Also the 4 and 4 can cancel, and we get

A =  L² – the simple and familiar formula for the area of a square!

Checking this for the triangle is more tricky because we to find the ‘normal’ area for a regular 3-polygon – or as we usually call it, an equilateral triangle.  For this we need our old friend, Pythagoras’ Theorem.

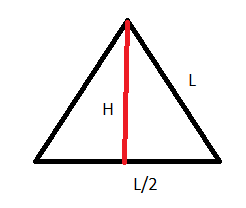Using the theorem in half the triangle, we get

(L/2)² + H² = L²

H² =  L² – L²/4  = 3L²/4

H = √3L/2

so A = √3L²/4

Now lets see what we get from our polygon formula with S=3.

Tan(180/3) = Tan 60 = √3

A = (L² x 3)/(4 x √3)

Remember that 3/√3 = √3

so A = √3L²/4

The same as with the direct method!

Conclusion

That, I claim, justifies my formula.  If anyone can think of an alternative way of finding the area of a pentagon or hexagon, then the formula can be checked for these shapes too.

Now, interesting things happen to our formula if S gets bigger and bigger, but that will have to wait for another post!