For today’s post I’m going to look at an exam question I saw posted on Facebook.

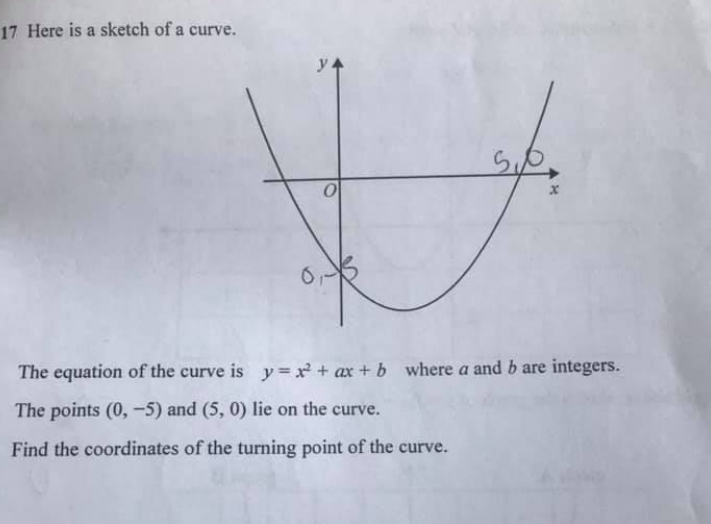
I confess this is the sort of stuff I get nerdy about! I love the way that equations can describe pictures, and vice versa.

 

 

 

Before we start, lets make sure we understand the terms used. What exactly is a ‘turning point’?   Well, it is the point where the line stops going down and starts going up (see diagram below).   That point at the bottom of the smile.

There are three different ways to find that but in all cases, we need to start by finding the equation – finding out the values of ‘a’  and ‘b’.

‘b’ is the easier. take the case where x=0 and the two terms with x can both be disregarded and so b = -5 = the point where the curve crosses the y-axis (also known as the line ‘X = 0’.  That is similar to the reason why the term ‘c’ is often called ‘the y intercept’ for straight lines, equation y = mx+c

The other point we know is (5,0)  so we can create the equation

25 + 5a – 5 = 0 (By substituting the value of 5 in for x)

We can solve this for a giving a=-4

 

The full equation is  y = x² – 4x – 5

I usually check my work at this stage  5² – 4 x 5 – 5 = 0 – as required

Now, I said there were 3 ways to find the turning point. I will give all three here bu, be warned, the third does require some A-Level maths. This diary is more aimed at GCSE students but method 3 is actually the way I would usually find the turning point, so I will give a brief description here.

Method 1 – The ‘parabola’ is symmetrical.

A Parabola is the name of the shape formed by an x² formula

 

On this version of the graph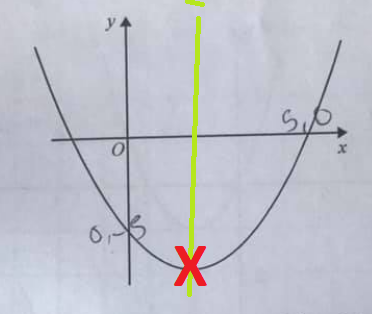

I’ve marked the turning point with an X and the line of symmetry in green. 

This tells us the value of x on the turning point lies halfway between the two places where y=0 (These are solutions, or roots, of x² – 4x – 5 = 0

We know one of these is is x=5. We can get the other by factorising  to give (x-5)(x+1) = 0. So x = -1 is the other solution. Halfway between x = -1 and x = 5 is x = 2.

when x = 2, y = 2² – 4 x 2 – 5 = -9.  So the turning point is (2,-9).

Method 2  Complete the Square

If we ‘complete the square’ on this equation we get

x² – 4x + 4 – 4 – 5  –  I’ve added in 4 and taken 4 away which looks like an eccentric thing to do, but this means we can factorise the first part into a square

(x – 2)² – 9 (also combined the -4 and – 5 to make -9)

This where we use our knowledge that a ‘square’ is never less than 0, but it can be 0. So its minimum value is when that square = 0 – so x – 2 = , so x = 2. And we can also see the value of the whole thing there is 0 – 9 = -9

Method 3 – By differentiation

This is A-Level stuff really, so I’ll only give an overview. This is the way I would usually do this, but then I have studied Maths through A-level (and beyond!)

Differentiation is one branch of Calculus, the mathematics of measuring change.

By a rule you will learn if and when you first study calculus, the equation of how much x² – 4x – 5 is changing is given by 2x – 4.

The turning point is where the line isn’t changing, so 2x – 4 = 0 (Zero change) so 2x = 4 and x = 2. y = 9 can be as above.

 

Summary

I’ve given three methods here. Fortunately they all give the same answer! (They wouldn’t be good alternatives otherwise!)

Choose which of the first two you feel most comfortable with.  The third method is the easiest to extend to where we have equations of than an a x²