As we get close to the exams, my students mostly want to do previous exam questions with me, so today I am sharing one which I found rather interesting – Algebraic proof. Perhaps because it foreshadows the kind of Maths one does at A-Level and degree level but its aimed at GCSE students.

The skills required are not that different to solving equations, but the level of thinking required is perhaps one level further on.

The question is…

Prove that the square of any odd number is one more than a multiple of 4.

The idea of an algebraic proof

The first thing to notice are those words ‘prove that’..  for students who are used to Maths being about doing a sum and finding an answer, this could seem quite new.  We are told what to expect. We just need to show the statement is true.

One of my students said ‘does this mean I have to look at every odd number’.  That would be quite difficult because there is a never -ending list of them. But its not a bad way to start, to convince yourself it might be true.

5² = 25  – and that is 1 more than 24 which is 4 time 6.

11² = 121 and that is 1 more than 120 which is 4 times 30

I could keep going like that – and you should do maybe a couple of your own – but I will never prove its true for ALL numbers like that.

 

What is easier : prove its true or prove it isn’t?

 

Its easier in Maths – and in life – to prove something isn’t true. We only need to find ONE odd number where the square is not 1 more than a multiple of 4 to prove that statement is not true*. A person only needs to show he was in Birmingham on Tuesday evening to show he didn’t commit the crime in Paris.

(*You could try but don’t waste your time looking,  it is true!)

Proving things are true is harder.  But we can still do it. We are going to do this with algebra, looking at the ‘general case’. That is why we call this algebraic proof.

We need to think of numbers more generally.  What is the ‘general’ odd number.  Take a number, any number. Will it be odd? Well there is a 50-50 chance.  But if we double the number we know it will be even (131 doubled is 262), then add 1. We then know the answer we get will be odd.

And in fact, all odd numbers can be found using  2n + 1 – That is a general odd number!!

So take our general odd number, and square it.  (2n+1)(2n + 1).  I could have written this with a ² but I find its easier to multiply brackets if you can see both.

We get

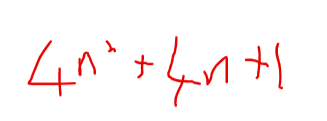
Factorise just part of this you get 4(n² + n) + 1

And that is actually what we are looking for! Let me explain. In 2n + 1, our ‘general’ odd number, n is just any whole number, and so n² + n is also just a  whole number.

So 4(n² + n) must be a multiple of 4 [ 4 times (n² + n)] and 4(n² + n) + 1 is 1 more!

This completes our example of algebraic proof.