Let’s consider this question from a Higher GCSE paper.

 

 

 

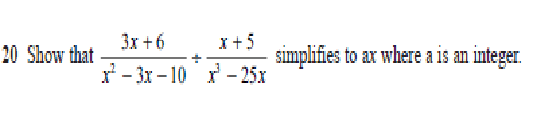
First thing I think is – Wow, that looks complicated.

[Actually, the first thing I should think is, what sign is that. It is a divide sum in the middle, not an add sign as I first thought]

Algebra fractions can stump the brighter students, but its worth remembering to rules are just the same as fractions with numbers.

We could do this divide sum by flipping the second and multiplying the numerators together and then the denominators. But given that we are told the final answer is simple, there is certain to be a lot of simplifying we can we first.

The first thing I noitices was that the bottom of the second fraction was going to factorise. It looks so close to the ‘difference of 2 squares’ rules.

Indeed it does factorise to

x(x+5)(x-5)

And immediately we see there is some cancelling to be done with the top to give 1/x(x-5) for the second fraction

What about the bottom of the first fraction. Looks like there could be some factorising to be done there. And indeed, taking my cue from the (x-5) we have already seen, this factorises to

(x – 5)(x + 2)

Something I missed before because I was so busy factorising the higher powers of x, but the top can be factorised as 3(x+2) and so we can cancel to

3/(x-5)

NOW we can do the divide by flipping the 2nd fraction, and the operation is now much easier than before

3/(x – 5) *  x(x – 5)   [Using an * for multiply here to stop confusion with the x’s]

which is then 3x = so a = 3.

 

 

;