Living on a higher dimension is something I am sure we’d all like to do; Well, if I meant a level of unbound wisdom; This is a Maths Diary, though, so I probably mean Dimension, as in shapes!
Maths students study shapes that have 2 or 3 dimensions. The underlying maths regarding shape can be extended to more dimensions.
For example, we all know the area of a square is L2 where L is the length of one of its sides The volume of a cube is L3, again where L is the length of one of the sides.
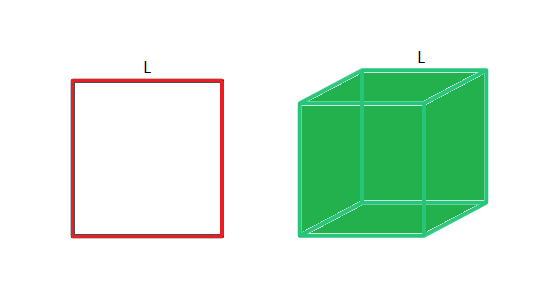
A ‘Cube’ in higher dimensions
So what does L4 represent? Its definitely something we can write down, but does it have a meaning. Its fair to say that, by extension this would be the ‘amount of space’ occupied by an equal-lengthed shape in 4 Dimensions!
The difficulty lies in trying to relate that to what we know, as we don’t know 4 dimensions. A 4-dimension cube is often called a hypercube. Another name for it is a Tesseract – and that is a word I’ve only just learnt!
Below is representation of one, but there is a problem with trying to show 4 dimensions, using just a 2-dimension screen. I’ve seen various ways of doing this, and the way I’m showing here is the clearest to me… Think of the ‘cube inside’ as being smaller only because its further away. Its really the same size.
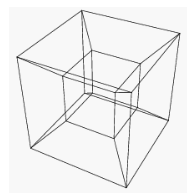
To an extent we also had this problem in drawing the cube, as shown above. There we were trying to show three dimensions on a two dimension screen. That was only a ‘gap’ of one extra dimension though, and we are familiar with what a cube looks like.
In my next post I will continue with this theme, and consider how we can show other 4 dimension shapes in two dimensions.
For more on Higher Dimensions, see my next diary entry