I’ve been looking at exam questions a lot recently in this diary – well it is coming up to exam time!

In June, the focus is going to be on famous Mathematicians, Over the summer I’m looking to write some entries on mathematical puzzles – If you know some good ones please send them in!

Today though, I’m looking at curves – the lines we can draw to represent certain mathematical equations.

In particular, today and tomorrow I am writing about curves that are ‘continuous’ and curves which are not, which we call ‘discontinuous’. Also, what that means for how we can use these curves to answer questions – That bit is for tomorrow!

What do I mean by continuous? Basically this means that an ant can follow the curve and get to all parts of the curve, without flying off the page or leaving the line. There is a Mathematically precise way of defining ‘continuous’ but I think my ant gives you the idea.

Lets look at some examples. (For this I am going to borrow screenprints from my favourite websites, the link on the Links page)

y = x²

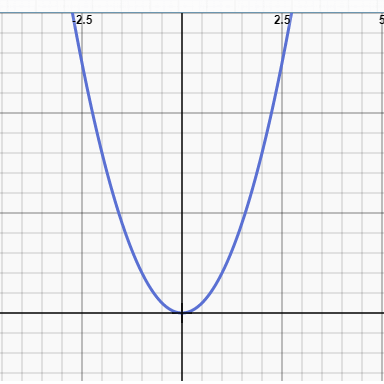
You can imagine the any being able to walk around this line. In fact any line of the form
Ax^a + Bx^b + Cx^c+ ….   will be continuous so long as a, b, c etc are positive integers.

 

 

 

 

y = sin (x)

 

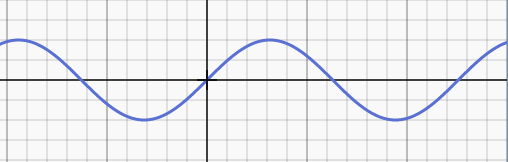
And again the ant can walk up and down these curves.

 

Since the line for y = cos x looks similar, we can say that is continuous too.

Lets have a look at some Non-Continuous curves now, The easiest to show is  y = 1/x

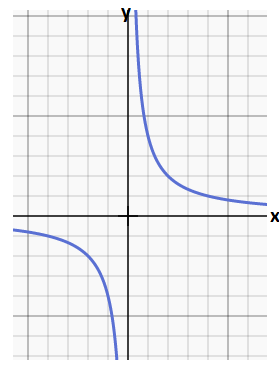
This curve is in two parts. Our ant isn’t going to get from one part of the curve to the other without a jump.

 

 

 

 

 

Going back to our trigonometry, Tan (x)  – unlike Sine and cosine – is discontinuous. There are many and regular breaks in the line.

 

 

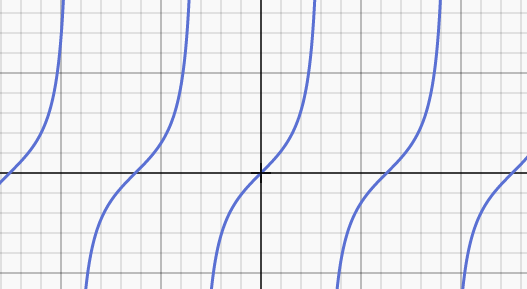
In tomorrow’s post I will look at some more eccentric examples and show why its important to understand if a curve is continuous or not.