In this entry I am going to look at ow to solve a Sudoku puzzle using Sets and Venn diagrams

What is a Sudoku Puzzle

Sudoku puzzles have now been around for over half my life, and sometimes I’ll have a go at one. They are not my favourite sort of puzzle but they divert the mind for a while.

If you do Sudoku, you may not realise it, but you are doing a problem in 3 dimensions. Each number has to be unique in three directions – in each column, in each row, in each box.

So that is one I did a few days ago – and yes, I did finish it!

Venn Diagrams

But before I describe how I went about that, lets track back and look about something I learnt in about Year 7 (or ‘First year seniors’ as we called it in my day!)

Actually I did ask my A-level student from 2 years ago about sets and Venn Diagrams – and he said he hadn’t learnt about them. But there are definitely questions about them on GCSE exams now.

Venn Diagrams were the invention of English Mathematician John Venn who was working about 100 years ago. They are the clearest way to show sets and how they relate to each other.

Let’s just step back one step first though. What is a set?

A set is just a collection of things. Of letters, of people, of cats… even of sets!  Let’s say set A is the ‘the set of all the vowels in the alphabet’,   B is the set of all the letters in the word FACE

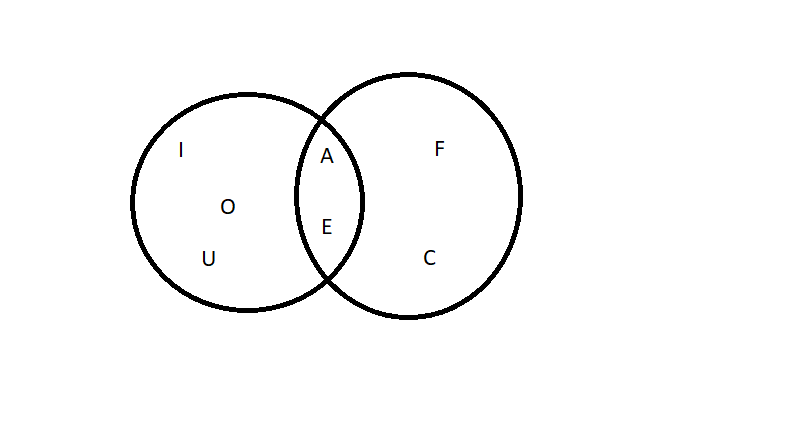This is a Venn Diagram showing set A and set B. The place to look is where the two circles overlap. In that space I have written the letters A and E because  they belong to both sets.

 

I said that the ‘things’ in the sets could themselves be sets themselves. That might sound like a strange thing to say.  But lets say C is the set of all the elephants in the world and set D which is ‘the set of all sets of animals!’.   Then set C would be in set D!

How to solve a Sudoku puzzle – using Sets!

Let’s get back to Sudoku. How can set theory help?

When I look on what number I can put into an empty square – let’s say the square in the middle of the second row

In this Venn Diagram, I’m defining the set ‘Row’ to be ‘all numbers that don’t yet appear in row 2. Likewise, the sets ‘Column’ and ‘Square’ are all the numbers that don’t yet appear in the 5th column and the top-middle square.

NOTE: I’ve said numbers are members if they DON’T already appear on the Row, column and square. That is because that is what qualifies them as the right number for the square.

The number 1 is already in the row, column and square.  But we can put the number 2 on the diagram. Its not in the column yet.

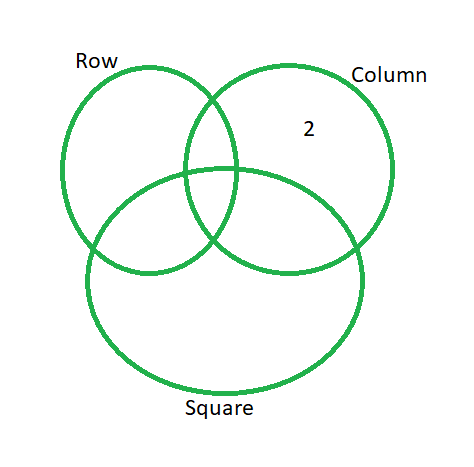
If I consider number 3 to 9 in turn and add them to my Venn Diagram, I get this

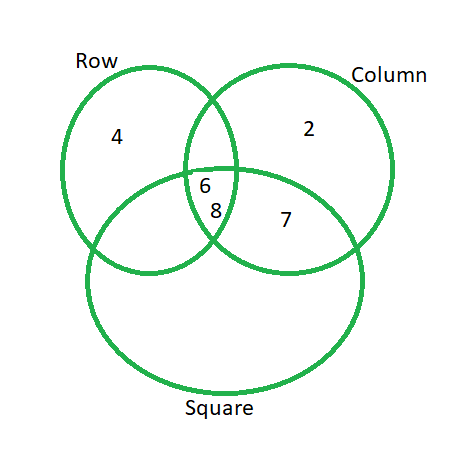
The right number to put in the box needs to qualify in all three ways. It needs to be in all three sets.   The middle of the Venn Diagram, where all three sets (i.e. the circles) intersect.   We actually have two numbers in that space. 6 and 8.  Actually that means we don’t yet know what number to put in this square. More of the puzzle needs to be solved before this box is.

Do I draw Venn Diagrams  for every blank square? Well, Ok, I draw them in my head, but my thinking follows the same line

I am solving a Sudoku puzzle using ‘Set Theory’