In this post I’ll look at the three different ways to solve a quadratic equation
Oh yes, Sorry, first post for a while. I spent much of February making videos for my Facebook Group (And yes, that’s a link to it!)
Let’s consider the equation x2 – 8x + 15 = 0
The first way we learn is to factorise, but spotting the factorisation isn’t always is easy or straightforward.
If you can’t see an immediate factorisation, you might want to reach for the formula, The formula has the advantages that it can always be applied – and can tell you quite quickly if there are real* solutions.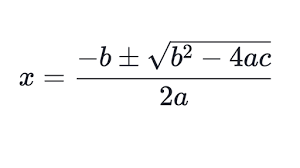
Its a good idea to work out the square root part first, as this will tell you if there are solutions and how many.
In this case : 64 – 4 x 15 x 1 = 64 – 60 = 4. The square root of 4 is 2.
(8 + 2)//2 = 5 and (8 – 2)/2 = 3
The fact that the solutions are integers suggests that the factorisation does exist, and we could have spotted it if we had looked a bit longer.
What numbers multiply to make +15? 1 & 15 and 3 & 5; and the negatives. Our numbers need to add to -8, so the ‘answer’ is -3 and -5.
The factorisation is (x – 3)(x – 5), and from that we can see the roots are 3 and 5. Roots is just a fancy mathematician way of saying the solution.
The last method is called ‘Completing the square’, which isn’t immediately obvious but is actually the way the formula can be found.
We take the number before the x (called the co-efficient) and halve it – In this case that gives us -4, which we write like this
(x – 4)2 – which can be expanded to x2 – 8x + 16
So how can we get from x2 – 8x + 15 = 0 to x2 – 8x + 16?
By adding 1 to each side to give x2 – 8x + 16 = 1, or (x – 4)2 = 1
Taking the square root of both sides gives x – 4 = +-1.
Add 4 to both sides gives x = 3 and x = 5
We get the same answer for the three different ways to solve a quadratic – but it would be awkward if that were not so!
For help on this and other Maths topics, see my current deals on Lockdown tuition.
One comment