I’ve been posting a lot recently on answers to GCSE questions – mainly because that is what I have been doing with students –  and I do have ten more days of that.

For today something different a look at something quite unusual…  As the title suggests – INFINITY.

Today’s post is based on some of the work of German mathematician Georg Cantor, a man not often understand by his contemporaries – In fact one said he was ‘aha ed of his time by one hundred years.

What Cantor was trying to do was explore what infinity means, and his revolutionary idea was that there is more than one infinity!  In fact…  there are an infinite number of infinities!

I’m not planning to show where they all come from in this post – I’ll just show that there is more than one.

 

 

If you go out with six friends this week, how will you know there are six of them? Well, OK, that seems like a simple question – because you can count, right?. Yes, but understanding how we can count is the starting point of understanding where all the extra infinities come in. You know you have six friends with you because you have given each a number, starting with 1..  and you got up to six! OK so may not have done that explicitly, but that is what you did.

And that is what we are going to use in a moment to demonstrate infinities.

Two quantities are the same if you can match up one item from one ‘list’ with one ‘item’ of the other… and have none left over. So the numbers 1 to 6 can be matched with your 6 friends with no numbers left over.

Now, this is where we come to some surprising ‘facts’…..  Ask,  are there more whole numbers than ‘even’ whole numbers.  You think, yes? Well look at this…..

 

 

 

 

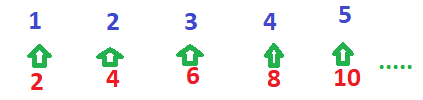
Even numbers can be paired up with whole numbers with no numbers from each group left out.  This is one of the surprising things we learn about infinity. The number of even numbers is the number all numbers.

Now imagine you are on a ‘chessboard’ floor that stretches for infinity in all directions.

How many squares are there. Infinity – or more than infinity. This, after all ‘infinity squared 

 

 

 

Let’s try counting the squares in the same way that we counted your friends.  Start with one square – it could be the one you are standing on. Thats 1.  Now count the 8 squares around you – 2,3,4… 8

Then the squares around that.

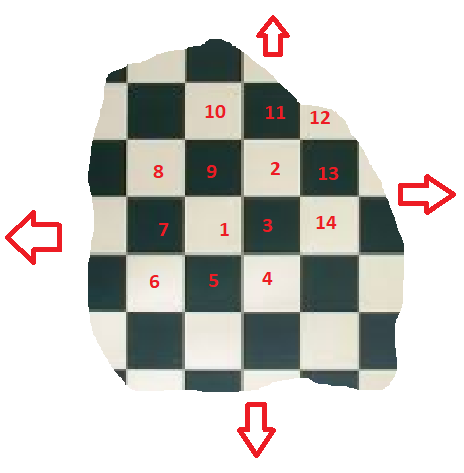
 You can keep going like that for ever  – but that’s OK, we can keep counting for ever.

So even on this infinite board, the number of squares is the same as the number of numbers – Infinity.

 

Now, at this point, if I didn’t know what was coming next, I might be starting to doubt my earlier remark – that there is more than one sort of infinity.

Lets consider now, decimal numbers, by which I mean numbers of the form

1.5434677654433345656

I have 20 digits after the pint there. Lets say we mean numbers that DO end, but we will not specify how many digits they have before they do.

So lets start with the number 1.5

Where do we go to next to count; 1.6  or 1.55? Or 1.5000000001.

There are actually an infinite number of next steps, and thats before we get off our first ‘square’.

And THAT is where the next order of Infinity comes in. Its not possible to ‘count’ the decimals  with the numbers 1, 2, 3 …….  even they go on for ‘infinity’.

There are more than infinity decimals!