Not because I’ve been watching election results today, but because I was discussing ‘powers’ with a student this week – Today’s subject is ‘powers of numbers’… Its the first of a two-parter.
Raising a number by a fraction
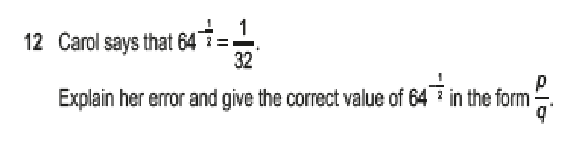
Before starting on the matters of powers, let’s consider the form of this question.
It’s another of those ones that suggests someone has done the question, and you have to give comment on their answer. In this case the question does say that Carol has made an error, but this won’t always be the case. I have done a question recently where the ‘answer’ given was correct, and the marks were to be gained by saying so.
With these question types, I think you just have to do the question yourself. You may be able to spot an error in something you haven’t tried yourself, but I’ll be honest, as a Maths tutor I can’t always do so myself.
Let’s get back to the question in hand and consider what a power means if is a) negative and b) a fraction – since in this case the power is negative and a fraction. I could tell you both answers, but I like to show how these answers fit into the wider picture.
You will recall that if were want to multiply two ‘powers’ together you can do this by adding the powers – so long as the ‘base’ is the same. The base is the number ‘raised to’ the power. In this case the base is 2.
22 x 23 = 25.
This makes sense when you think of 22 as 2 x 2 and 23 as 2 x 2 x 2. Put the big multiply together as
2 x 2 x 2 x 2 x 2 and you can see this can be written as 25
That rule of powers works well when the powers are positive whole numbers. What we want is for it to work with other numbers.
Powers of 0 and 1
First we need to consider two special cases.
What does 21 mean? And what does 20 mean?
21 means 2 multiplied together one time – and that is just 2! Remember this holds for all base numbers and you can’t go wrong.
41 = 4 361 = 36 40001 = 4000
With 20 we want to keep to the ‘adding indexes’ rule so that
23 x 20 = 23+0 = 23
8 x 20 = 8 – We can soon see that for this to work, 20 must have the value 1
Again, that works for all numbers
40 = 1 360 = 1 40000 = 1
Now we know what powers of 0 and 1 are, can you see what consequence this has for negative and fraction powers? This is what I’ll be looking at in the next post.
More details on this subject can be found here