Today’s post is about an exam question about a speed time graph I  was prepping for my students yesterday. I was surprised to see this question because it covers two points I associate more with A-Level work.

 

What can we find from the area under a curve?

 

a)  Area under the curve as the distance
b) Using the ‘ trapezium rule’

Before I say more, here is the question

 

 

 

 

 

 

 

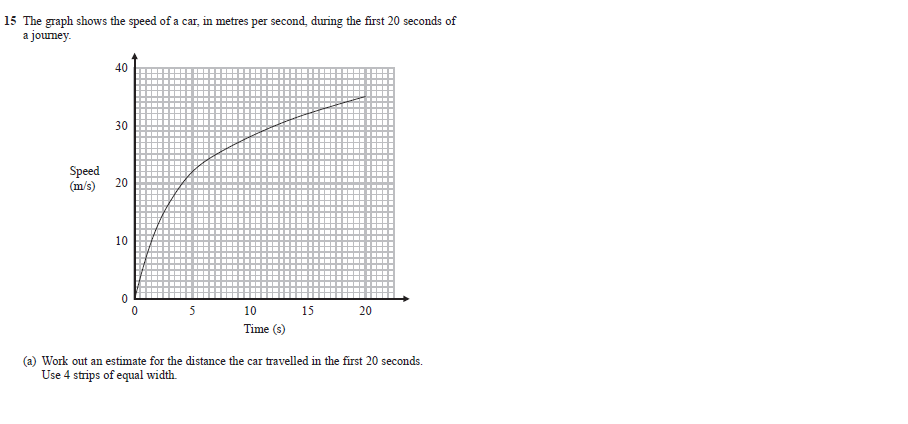
The question asks for the distance the car travels, but the graph is of speed over time. This is where the first of my ‘surprise facts’ comes in – You can find the distance travelled by measuring the ‘area under the curve’. I won’t here show why that is the case – that is for A-Level students (OK I might post on that later). For now though, I will just apply the rule.

The area ‘under the curve’  is the area of the shape made by the curve at the top and the line ‘speed = 0’ at the bottom, bound to the left and right by the times we are interested in : In this case t=0 and t=20.

The Trapezium Rule

We can only estimate the area of this shape, given how irregular it is – the top side anyway – and this is where the ‘Trapezium rule’ comes in. To apply this we have to divide the area into strips, each one a trapezium (OK, the first one is a triangle, but we can apply a similar rule. To be fair, the question does give a clue to what to do by saying we should use ‘4 strips of equal width’

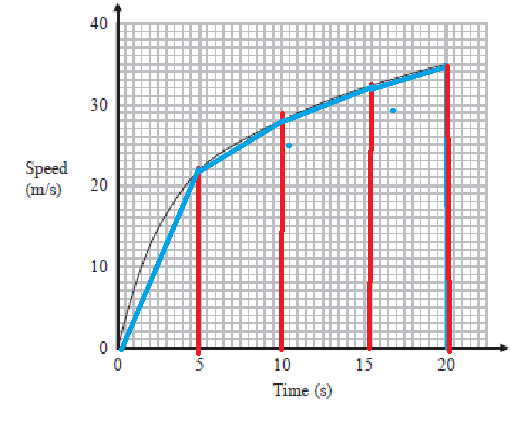We divide up like this.

The first area is a triange with area

1/2 x 5 x 22*

*The value of the speed at t=5

 

The other areas are trapeziums with area 5 x 1/2(Height at start + height at end).

The ‘height’ in each case is the speed values at t= 10, 15 and 20.

If we look at the calculation closely we can save time by noting the middle times are included twice each, 1/2 each time.

so the area of the trapeziums are 5 x (22 + 28 + 32 + 35 x 1/2)

This is a quicker way that fiddling about with all the 1/2s. The 35 – value at t=20 – still needs the 1/2 because it is a measurement only on one trapezium.

We get the value 5 x 99.5.   This is where I took into account that we are only estimating, so using a value of 100 instead of 99.5 is justifiable.    This gives us an estimate of 500m

There is a part(b) for this question on the next page.

Over and under estimates

 

“Is this an over-estimate or an under-estimate for the distance. Give a reason for you answer.’

 

The answer in this case is that it is an underestimate, because all those trapeziums still left a small space under the curve. I don’t think our rounding up to 500m stops this being the answer.

 

More about the trapezium rule can be found here