Yesterday’s post built up some of the things we need to answer a question where the power is negative and a fraction.

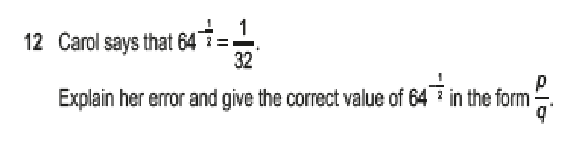
One key point is that for all numbers n

n⁰ = 1  and n¹ = n.

With negative powers we still need to maintain the rule of adding powers.

2^x x 2^-x  = 2^x-x  (and since x – x x = 0)  = 2⁰ = 1

Re-arrange this and we get  2^-x = 1/2^x

And there the first new rule – a negative power is 1/the positive power

3² = 9 so 3^-2 = 1/9

To get the second rule we need to consider how powers can be combined.

(n²)³ = n⁶  – When you raise a power to a power – multiply the powers

[Consider  n x  n     x     n x n     x    n x n]

 

Now look at

(n²)^1/2  =  n¹  = n

So what does raise to power of half mean if this involves getting from n² to n?   Taking the square root!  We could replace 2 and 1/2 with 3 and 1/3 – so see n^1/3 means take the cube root – and so on.

n^1/x means take the xth root of n.

Just before we get back to the question given, lets just complete the patterns by considering what x^3/2 means. I have seen some exam questions that do pose questions like this.

I suggest you split the 3/2  into  1/2 x 3  or,  n^3/2 = (n^1/2)³

so 4^3/2  =  (sqrt(4)³)  = 2³ = 8. It is generally easier to take the ‘root part first. In a non calculator paper you’ll only be asked about roots you know.

Let’s get back, at last, to the original question.

64^-1/2–   Take the 1/2 part first, that means square root, and the square root of 64 is 8.  The – part means take the reciprocal  1/8

What Carol did was take 1/2 of 64, not the square root of 64, so your answer should include a sentence.  ‘Carol didn’t know that a power of 1/2 means square root, not multiply by 1/2’ – then give the correct answer of 1/8.

 

I’ve made this into 2 blogs posts with lots of background but if you can remember the rules given in these posts, this question need not take you long in an exam,