More on Angle types

In the last post I started to describe how patterns in angles can help us find the size of missing angles without doing any measuring. In this post we look at two more angle types. First I will show what we mean by Corresponding and Alternate angles.

Then I will show how we can put all this together to answer a question.

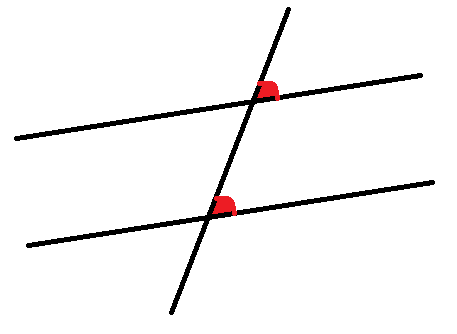
For both of these situation, we need one line crossing two others which are parallel.  If we don’t know the two lines crossed are parallel, we can’t use these rules, got it?

And you know how to tell if two lines are parallel? The two lines are never going to meet, however far we extend them.

So, the two angles marked in red – they are going to be equal.  So if we are told the lower one is 50˚  then the higher one is also 50˚.

These is what are called ‘Corresponding angles’

This is like the rule in the last post where we know two angles must be the same if they are ‘opposite’. Angles are also the same if the are ‘corresponding’

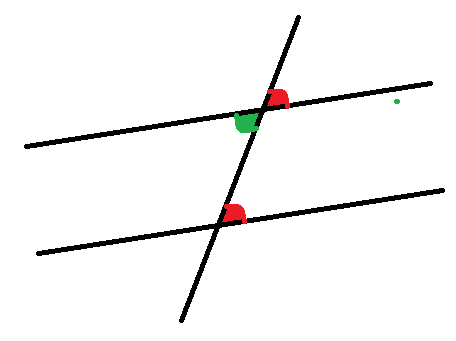Now look at this diagram.

The two red angles are ‘corresponding’ and the green angle is ‘opposite’ one of the red angles.

So all three angles will be the same.

We say the bottom Red angle and the green angle are ‘Alternate’.  ‘Alternate’ is like a combination of the ‘Corresponding’ rule and the ‘Opposite’ rule.

Some people think of this as the Z rule – because the angles in a Z are the same.

That’s alternate angles

I’ve been looking for an exam question that uses all of these but they are hard to find, and I only want one for this post, which would be too long otherwise…  so…  let’s have a look at this

 

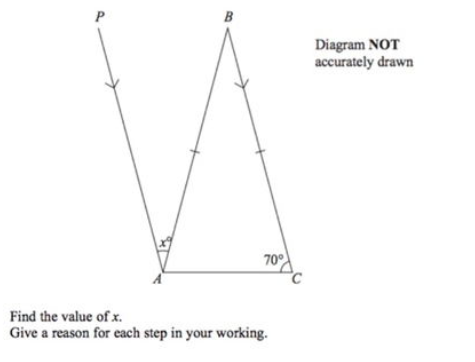
A few points about the wording and notation here
1. I across two lines shows those lines are of equal length : AB = AC
2. > on two lines shows they are parallel. AP is parallel to CB
3. ‘Diagram Not Drawn to scale’ means take the information given as true. Don’t check them with your ruler or protractor.

ABC is an isosceles triangle, so <ACB = <CAB = 70˚.  < ABC = 180 – 2 x 70 = 40˚ – because of angles in Triangle ABC add to 180˚

<BAP = <ABC because they are Alternate – (to see the Z shape turn it round a bit)

So x = 40.