This  posts uses Similar triangles to solve a question that was posted in a Facebook group for tutors.   I thought it was fun so I’m sharing it here.

My answer uses the idea of Similar Triangles. If you are not sure what they are, click here.

My first thought on seeing the question was that similar triangles were involved but I didn’t realise they were studied before 11.

Anyway, here is the question.

 

 

 

 

 

 

 

 

 

 

 

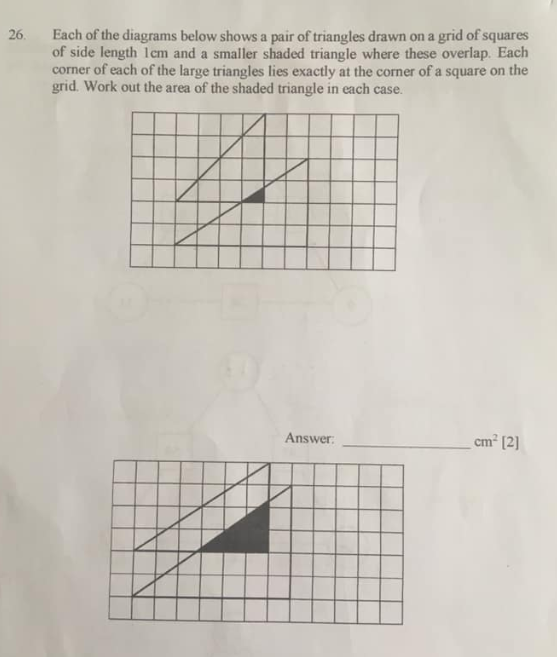
There are two parts but the method is the same in both. You can just look at one of the lower triangle and the overlap. The whole of the other triangle can be disregarded

Solution to similar triangles question

The key is seeing that the shaded area is ‘similar’ to the lower triangle (or the other one).  We can show they are similar because all the lines are parallel, so the angles are the same – corresponding angles

Both Triangles have a vertical line and a horizontal line, so those two pairs are parallel, and the two hypotenuses are ‘parallel’ as they are part of the same line.

As they are similar, the sides must be in the same ratio.  The ratio between them can be seen most clearly by comparing the lengths of the bases….  6 for the bottom triangle, 1 for the overlap

So the ration is 6:1. The lower triangle has height of 4,  so the height is 4

4/6 * 1 – or 2/3 a square.

The area is 1/2 * bh – so that makes 1/2 * 1 * 2/3  = 1/3 cm²

The second Triangle

 

The method for the second triangle is the same.  here the ratio is 7:3 and the height of the lower triangle is 5cm.

Using the ratios we can see the height of the overlap is 3/7 * 5 =15/7

The area is 1/2 * 3 * 15/7 = 45/14 cm²

 

In this entry I am going to look at ow to solve a Sudoku puzzle using Sets and Venn diagrams

What is a Sudoku Puzzle

Sudoku puzzles have now been around for over half my life, and sometimes I’ll have a go at one. They are not my favourite sort of puzzle but they divert the mind for a while.

If you do Sudoku, you may not realise it, but you are doing a problem in 3 dimensions. Each number has to be unique in three directions – in each column, in each row, in each box.

So that is one I did a few days ago – and yes, I did finish it!

Venn Diagrams

But before I describe how I went about that, lets track back and look about something I learnt in about Year 7 (or ‘First year seniors’ as we called it in my day!)

Actually I did ask my A-level student from 2 years ago about sets and Venn Diagrams – and he said he hadn’t learnt about them. But there are definitely questions about them on GCSE exams now.

Venn Diagrams were the invention of English Mathematician John Venn who was working about 100 years ago. They are the clearest way to show sets and how they relate to each other.

Let’s just step back one step first though. What is a set?

A set is just a collection of things. Of letters, of people, of cats… even of sets!  Let’s say set A is the ‘the set of all the vowels in the alphabet’,   B is the set of all the letters in the word FACE

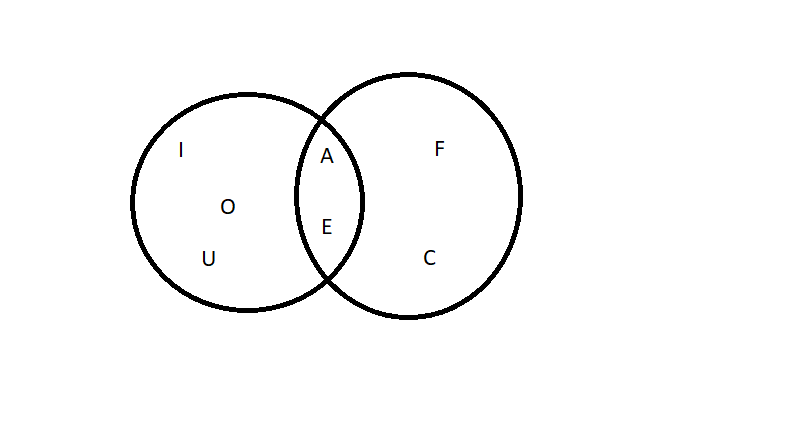This is a Venn Diagram showing set A and set B. The place to look is where the two circles overlap. In that space I have written the letters A and E because  they belong to both sets.

 

I said that the ‘things’ in the sets could themselves be sets themselves. That might sound like a strange thing to say.  But lets say C is the set of all the elephants in the world and set D which is ‘the set of all sets of animals!’.   Then set C would be in set D!

How to solve a Sudoku puzzle – using Sets!

Let’s get back to Sudoku. How can set theory help?

When I look on what number I can put into an empty square – let’s say the square in the middle of the second row

In this Venn Diagram, I’m defining the set ‘Row’ to be ‘all numbers that don’t yet appear in row 2. Likewise, the sets ‘Column’ and ‘Square’ are all the numbers that don’t yet appear in the 5th column and the top-middle square.

NOTE: I’ve said numbers are members if they DON’T already appear on the Row, column and square. That is because that is what qualifies them as the right number for the square.

The number 1 is already in the row, column and square.  But we can put the number 2 on the diagram. Its not in the column yet.

If I consider number 3 to 9 in turn and add them to my Venn Diagram, I get this

The right number to put in the box needs to qualify in all three ways. It needs to be in all three sets.   The middle of the Venn Diagram, where all three sets (i.e. the circles) intersect.   We actually have two numbers in that space. 6 and 8.  Actually that means we don’t yet know what number to put in this square. More of the puzzle needs to be solved before this box is.

Do I draw Venn Diagrams  for every blank square? Well, Ok, I draw them in my head, but my thinking follows the same line

I am solving a Sudoku puzzle using ‘Set Theory’

 

 

You probably saw questions ‘What is the next number in the sequence?’   quite early in studying numbers.

Next number in a sequence example

2  4   6   8   10  ..  what is the next number?

 

Let’s just ignore the people who can see the answer straight off,  and look for a method.

Look for the GAPS between each number. That is always the best start. In this example, the gap between each number is 2 – To put it another way, the numbers are going UP by 2 each time.

Once we have spotted that, we can move on through the sequence, adding two onto the last number each time.

… 12  14  16

Where we can get clever though is trying to find a general term in this sequence.  This is a step up in effort, for sure.

What we do here is give all the numbers in a sequence a ‘place in the  sequence’   which we do, in true algebra fashion, by using a letter. Its normal to use n in sequences.  Questions will usually ask ‘find the nth’ term?’

We say we the first term in the sequence is n=1,  then n=2 for the second, and so on.  The general term then uses n in a formula. Let’s see how its done

Finding the nth term

The first thing is to see the gap, as we saw before. In the first example, the gap was 2

1  4  7 10 13

In this sequence the gap is 3

So we start our nth term formula by putting this gap number in front of the n.   2n for the first example,  3n for this example.

So – does ‘3n’ give the sequence we’ve been asked to investigate?

No, because that sequence is

3  6  9  12 15 ..

But we can compare the two sequences – something we do a lot when looking for nth term formulas – and see our sequence is 2 less for eeach term than 3n: 3 6 9 …

so we have our formula   3n – 2

We can check, say, the 5th term  –   5 x 3 – 2 = 15 – 2 = 13. That matches what we were given. We can now confidently predict the 100th term

100 x 3 – 2 = 200 – 2 = 298

Is the number in the sequence?

Another common question is – is 100 in the sequence 1 4 7 10….

This question has not asked you to find the nth term – but that is the route to finding the answer.

We have already found the nth term for this sequence. This means we need to find n where

3n – 2 = 100.

We start to solve this like an equation, by taking 2 from both sides

3n = 98.

Now we hit a hitch.  n is not going to be a whole number because 3 is not a factor of 98.  In sequences we are only interested in cases where n IS a whole number.

from this we can say that 100 is NOT in the sequence because there is no n where 3n – 2 = 100

More Practice

For more practice, see this website

 

In today’s post I will be looking at how to Combine Powers. By a ‘Power’ I mean that little number you sometimes see at the top right of a number.

So – What does it mean?

3²  is another way of writing 3 x 3.  ‘Squares’ are quite familiar. But we can extend this idea

56  =  5 x 5 x 5 x 5 x 5 x 5 –  count the 5s – there are 6 of them!

And with that, you can probably how to see how any other ‘power’ calculation can be worked out, like 23¹⁵⁰ or 31²⁴⁵ – though you’ll understand if I don’t write those out in full!

Answers to ‘power’ sums can get very big!

By the way, sometimes you will see the word ‘index’ and that means the same thing. And sometimes its called ‘order’, which explains why it is an O in the acronym BODMAS.  If you are not sure what I mean by BODMAS, check here

How to Combine Powers

Once we understand how something is written in maths, the next step is to see how we can combine powers. How does this idea with things we already know?

For example – what does it mean if we write  6³  x 6⁴

The easiest way to see how to make sense of that is the first write this out in full

6 x 6 x 6    x   6 x 6 x 6 x 6  –    and now we have 7 6s  – all times together –  So we can write this as 6⁷

6³  x 6⁴ =  6⁷

Now, we don’t want to write things out in full every time, so lets look at what we have really done. Then we can see a short cut.

3 + 4 = 7!  So we can see a rule that might come from this. If you want to multiply power, just add the powers together.

Note that we can only do this if the bigger number is the same. We can’t add the powers and get any sensible answer if we try

5⁴ x  7³ – where the 5 and 7 are different. There is a way I would simplify that but I won’t look into that now.

Some special cases

One last thing for today,  I’d like to consider what 2¹, 2⁰ and 2^{-1 all mean.}

What does it mean to say ‘Multiply 2 and 2 and 2… -1 times! Doesn’t seem to make much sense, does it? But we can see how these things can mean something if we look again at our rule to combine powers.

So that’s not what we do, but we do want our rule of Index Adding to mean multiplying to still work.

So lets look at

2² x 2¹ = 2³

and 2² x 2⁰ = 2²

and 2¹ x 2^-1 =2⁰

The answers I’ve shown here have been worked out by the ‘adding powers’ rule – e.g. 2 + 1 = 3

The first one is the easiest to explain –
2 x 2    – how do we get that to 2 x 2 x 2 ?  By multiplying by 2 again!

so 2¹ = 2. That makes sense if you can get the sentence  2 multiplied together 1 time!

But what does it mean to say ‘2 Multiplied together 0 times’?

2² x 2⁰ = 2² – But what number doesn’t change others in multiply sums?

The only number that does that is 1…  so it can only make sense that 2⁰ -1

In fact, this is the rule for all numbers 5⁰ = 1 43⁰ = 1 – and so on.

This takes me to my special case, which complete the picture on how to use powers.

2¹ x 2^-1 =2⁰

Using the other two cases we can rewrite this as

2 x 2^-1 = 1

from that we can see 2^-1 = 1/2 – because thats the only number that completes this sum

We can extend that idea to say any ‘-‘ power  – just put the number on the bottom of a fraction with 1 on the top

So 14^-12 = 1/14¹²