My second post on avoiding and correcting errors seems a bit obvious! Its very important to actually read the question. But it doesn’t stop many people, including myself from forgetting this ‘tip’ from time to time!

It’s time to read the question!

I’ll show this by an example from the exam paper I’ve just completed.

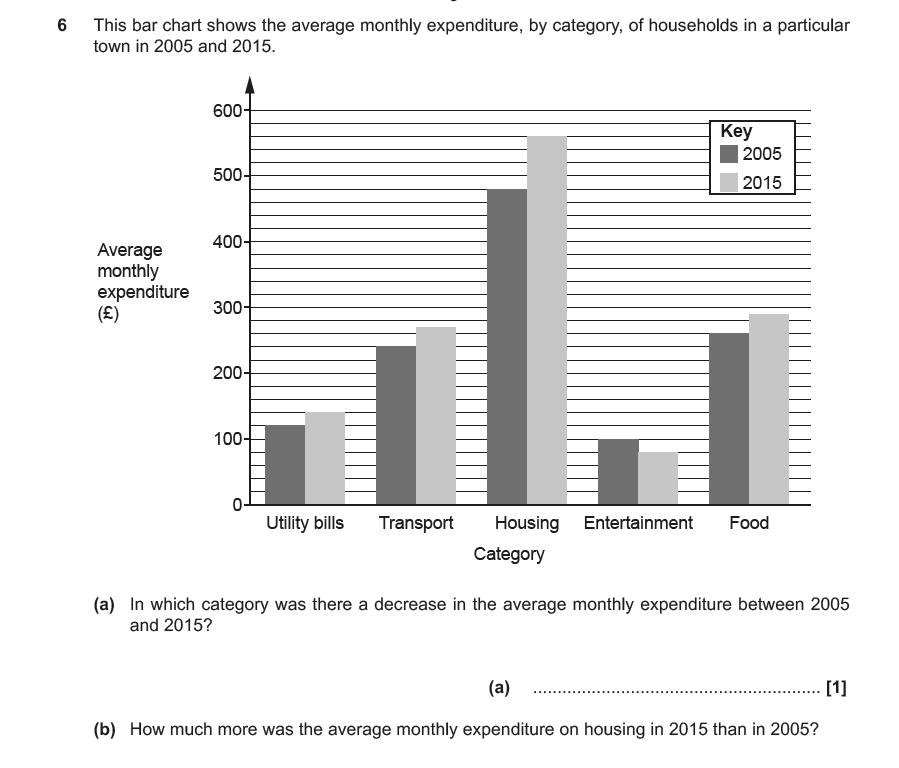
The first part I answered correctly – see if you can!

Spot the difference!

Its the second part I am writing about here.  Now I know why I made the mistake. I’d tutored students many times before on questions like this – or so I thought – and I wanted to show off!

I read the question as ‘What was the difference in Monthly average expenditure’ between the two years. I have seen students answer this question before – when it was the question asked – by reading off all the data, adding all the numbers together and comparing.

And I usually tipped the more able students that they don’t have to do this. Its quicker to find the difference in each column and add these up. So that is what I did now….

Have you seen this question before? Are you Sure?

Thinking you have seen the question before, like this, is a common reason for misreading – And its an error that is going to effect more able students, or at least ones with a good memory!

But this won’t help when the marks are added up.  Its the questions where you think ‘Oh, I know what to do with this one’ that you need to be most careful with, because they are the ones you are more likely to rush into without proper reading

OH, and have you spotted the important detail I missed in the question?

You will see I did too much work, and would have got no credit for it.

If you’d like to see my other post on very basic errors, then follow this link

I’ve completed  a couple of Foundation exam papers this week, as a bit of forward planning for one of my students – and when I came too compare my answers with the official ones,When I looked at my answers I saw I’d made some mistakes, so this is an entry about correcting maths mistakes.

In this post, though, I’d like to share with you a question that I did get wrong initially, but where I spotted my own mistake.

The thing is – My answer just didn’t seem right.  And that’s what I’d like to share with you in this posts – It’s a very important skill with number questions; To be able to feel when your answer feels right.

This is the question

To make this comparison, you need to work out how much one biscuit cost.

For the 20 Biscuit tin the sum is  £1.50/20. Although this is from a calculator paper, I did this ‘long hand’ and got the answer 7.5p each.

Next I did the calculation for the second tin, again ‘long hand/in my head’  and got the answer 5p per biscuit.

I don’t know how I did this – I made a mistake, and I never pretend I never make mistakes. I just wasn’t taking care.

But what I can do is think ‘Um, that doesn’t seem right. The second box costs a bit more than the first, and has slightly more biscuits.’

The answer just had to be about the same, not as different a 5p and 7.5p. That might seem like a big difference, but 7.5p is 50% more.

So I did the answer again, and found the cost per biscuit was also 7.5p each. The answer was that Nada was wrong, box 2 offers the same value, not better.

This might not work every time – If my wrong answer had been 7.4p per biscuit I may not have spotted my mistake.

But you would be surprised how often just thinking as you write your answer ‘does this make sense’, you can spot some basic errors. Correcting Maths mistakes is essential if you are to get the grade you deserve : Don’t let it effect your grade.

Here is some more useful advise on avoiding errors

Continuing yesterday’s theme of higher dimensions, in this post I look at a couple more 4 Dimension shapes and how they can be represented on a screen.

Thinking about how to show 4 dimensions its helpful to think of ways to show 3 dimensions on a 2D screen. One such way is to take ‘cross sections’.  For example, one way to show a cylinder is a series of circles.  Stack these together and you get a cylinder.

A cross section of a 4 Dimension shape will be a 3 Dimension shape,

Another way of thinking of this is to consider time as the forth dimension*.  Imagine seeing a sphere appearing as a dot, then growing to ‘full size’, then disappearing again at the same rate.  The diagram here would show stages of the process.

I’ve seen other representations of a ‘hypersphere’ but this is the one clearest to me.

How would a ‘Hypercube’ look like, using the same ‘cartoon technique?

(*Some people think this to be the case, through the 4-Dimension space-time physicists work with isn’t that simple, but it will do for this thought experiment).

Before we move off 4-Dimension shapes, I’d like share one of my favourite shapes. This can only exist if we have 4-Dimensions (The closest 3 dimension idea is a mobius strip)

In the picture, it looks like the bottle goes ‘through itself’. In the ‘4 dimensions’ this would not be the case.  Rather like if we want to get past a wall we step over it, using the third  dimension that a creature who knew only two dimensions could not

For more information on 4-dimensional shapes look here

Living on a higher dimension is something I am sure we’d all like to do; Well, if I meant a level of unbound wisdom; This is a Maths Diary, though, so I probably mean Dimension, as in shapes!

Maths students study shapes that have 2 or 3 dimensions.  The underlying maths regarding shape can be extended to more dimensions.

For example, we all know the area of a square is  L² where L is the length of one of its sides   The volume of a cube is L³, again where L is the length of one of the sides.

A ‘Cube’ in higher dimensions

So what does L⁴ represent? Its definitely something we can write down, but does it have a meaning.  Its fair to say that, by extension this  would be the ‘amount of space’ occupied by an equal-lengthed shape in 4 Dimensions!

The difficulty lies in trying to relate that to what we know, as we don’t know 4 dimensions. A 4-dimension cube is often called a hypercube. Another name for it is a Tesseract – and that is a word I’ve only just learnt!

Below is representation of one, but there is a problem with trying to show 4 dimensions, using just a 2-dimension screen.  I’ve seen various ways of doing this, and the way I’m showing here is the clearest to me… Think of the ‘cube inside’ as being smaller only because its further away. Its really the same size.

To an extent we also had this problem in drawing the cube, as shown above. There we were trying to show three dimensions on a two dimension screen.  That was only a ‘gap’ of one extra dimension though, and we are familiar with what a cube looks like.

In my next post I will continue with this theme, and consider how we can show other 4 dimension shapes in two dimensions.

For more on Higher Dimensions, see my next diary entry

The question is –  Does the rule for order of calculation, BODMAS  always apply?

(OK so it’s a bit eccentric having a post about Christmas at the start of August, but I liked the title so I am sticking to it)

For a reminder of what the BODMAS rule is,  check here

Can we ever bend the BODMAS Rule?

Well the real answer is ‘yes’ – but should the rules should be bent sometimes?

This idea started with a post I saw on Facebook. I gave my initial answer yesterday. This morning I had to admit I got it wrong, if we follow BODMAS to the letter.

A BODMAS Example

The question is, simply, what is the value of

Add 2 + 2 to get 4; multiply by the 2 outside the bracket and get 8;  then 8 divided by 8…  we get the answer 1.

Actually, by BODMAS rules the divide should come before the multiply (D before M)   so it should be 8 divided by 2 (Giving 4)….  4 x 4 = 16

That is probably the ‘Correct’ answer and I had to accept I was wrong  – and there is nothing bad about accepting one is wrong sometimes

Why I might disagree?

But I still feel somewhat attached to my original answer!  To me,  2(2+2)  LOOKS like a single unit for calculation. If the x sign had been there between the first 2 and the ( , as below, I don’t think I’d have made the same mistake

For me, the () is such a powerful sign,  I see any digit next to it as ‘belonging’ to it, and hence how I did that calculation in the way I did. I can’t claim that is the official rule; just the way I read it.

So my recommendation is, BODMAS rules as they are, if you want to communicate a calculation, if there is any doubt on what you mean, include extra brackets to avoid confusion