Growing up , Loving maths, I found out a few things for myself, and I’ll post about one of those next time.
But this is a simple rule with numbers my Dad showed me. Try adding up the odd numbers one by one, and see what you get
1 = 1
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25
You will recognise these numbers – all the squares! And this is the secret behind a type of questions I’ve seen on exam papers recently

There are a lot of different sequence questions, and its best not to leap in until you have really recognised. But if nothing appears to you, a next step is to look at how the numbers are increasing. Actually write the numbers in the gaps. If you worked them out in your head you might not see the pattern.
Here the gaps are : 7 11 15 19
And you will see straight away they are increasing steadily – By 4 each time. – And when you see this – that the second level of differences are constant – you will know you have a ‘quadratic’ sequence.
That is to say, the expression in terms of n will be of the form
an2 + bn + c – where b and c could be 0 but a is not (If a was 0, the first differences would be constant)
If you play with these sequences for long enough, you will find something very interesting but for this posts I’ll let you in on the secret
To find what a should be, take half of the ‘constant’ you find by following the differences. In this case that was 4, so a = 2.
So our sequence rule starts 2n2
We are now going to write our sequence again, and underneath, write double the square numbers
4 11 22 37 56
2 8 18 32 50
Takes away the bottom from from the top, you get
2 3 4 5 6
or n + 1 for each position
This means our full answer is
2n2 + n + 1
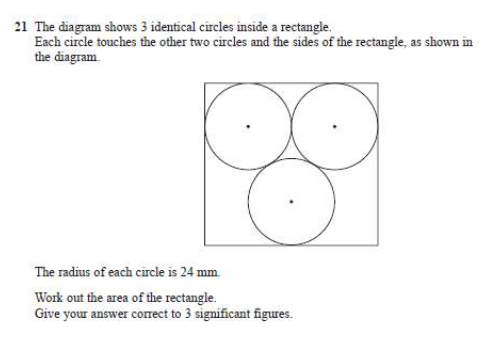 To find the area of the rectangle we need to find the length of the rectangle and its height.
To find the area of the rectangle we need to find the length of the rectangle and its height.

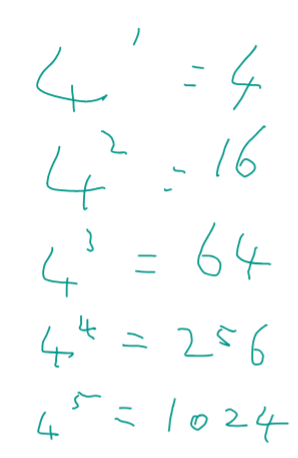
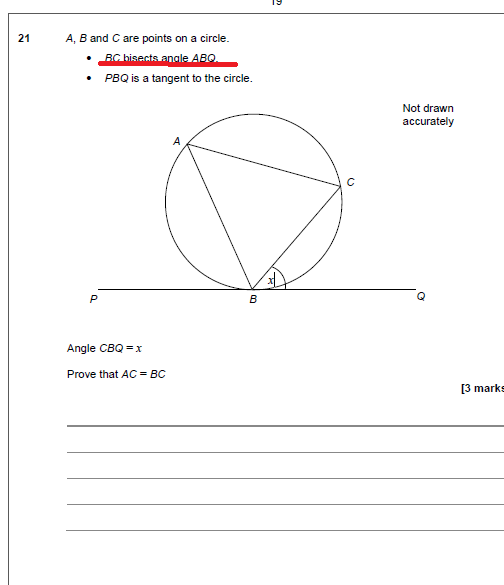 In my last post I described a question where I couldn’t see the answer.
In my last post I described a question where I couldn’t see the answer.