For this post, you need to know your basics in rounding numbers. Here is a recap
- Pick out the digit in the last place that will survive the rounding process
33962
- Look at the next digit… Is it a 0 1 2 3 or 4? If so take no action. Otherwise raise the underlined digit by 1. In this case a 9, so raise to 4
- In both cases, remove all following digits after the underlined one
34
Now, for this subject of bounds we are going to look at this kinda back to front. We are told a number has been rounded to 2 decimal places. So what could that number be?
2.335 is the smallest number it could be. Any number smaller would be rounded to 2.33
2.34499999 is the largest number it could be. Any number larger would be rounded to 2.35.
2.335 and 2.3449999 are the upper and lower bounds to the number given the information we have.
Let’s look at something a bit more complicated
Now, if we know that I have ran 10.6m to 1 d.p in 19.5 seconds to 1 d.p, then what is my highest possible speed and lowest possible speed, to 3 d.p ?
We are being asked for the ‘upper bound’ and ‘lower bound’ for the speed.
Remember Speed = distance / time
Start by writing down the upper bound’ and ‘lower bound’ of my distance and time.
Upper Bound of distance is 10.6499m
Lower Bound of distance is 10.5500m
Upper Bound on Time is 19.5499 seconds
Lower Bound on Time is 19.4500 seconds
Now, this is where we have to think because to find the upper bound on the speed, we need the highest possible time BUT the lowest possible time. This is because as time goes up, speed comes down, for any given distance. I use the highest possible value for time in the lower bound calculation, for the same reason
So upper bound on Time = 10.6499/19.4500 = 0.547553
The lower bound on time = 10.5500/19.5499 = 0.539645
The bounds for the speed are [0.540, 0.548] to 3 d p
Note that I used 4 d.p. in my calculations. I will always use one or more decimal places than required then round at the end. We risk losing accuracy otherwise.


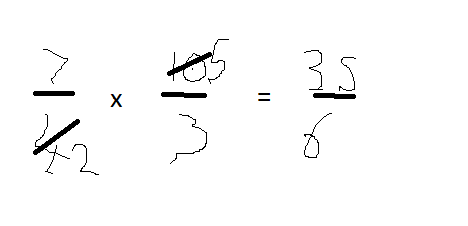 In this pic you’ll see I’ve converted the two numbers into 7/4 and 10/3 – done just a little cancelling, and then multiplied
In this pic you’ll see I’ve converted the two numbers into 7/4 and 10/3 – done just a little cancelling, and then multiplied