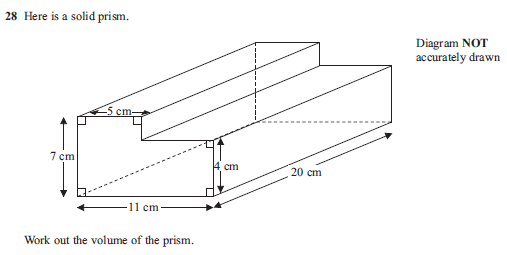
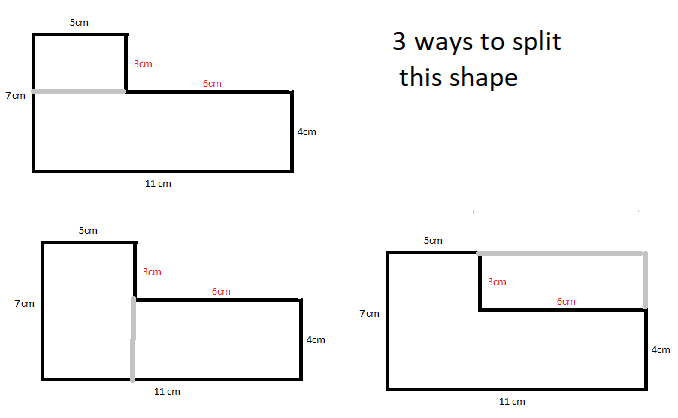
Today we look at another exam question, where we are asked to work out those angles. Or at least one named angle
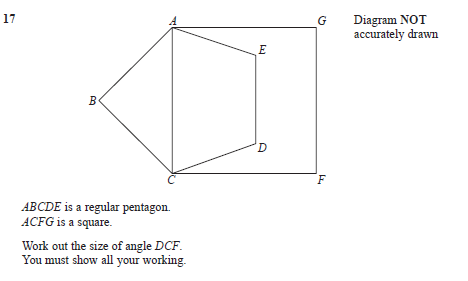
I was working on this question with a student a couple of weeks ago, and he worked out the answer quickly, but wasn’t quite able to describe why…. so this one is for you, Joe.
For a question like this, we do need to show we understand the reasons why each stage of the answer works. Relationships between angles often have names (Complimentary angles, Associate Angles) but we don’t need to know these for this question.
We do need to know.
- Angles in a triangle add up to 180
- Angles in a pentagon add up to 108. (That might not be as widely known, I’ll cover this in a later post)
- Sides in a regular pentagon are all the same
- Two angles in an isosceles triangle are the same.
- Angles in Right angle add up to 90.
So these are the steps that Joe took, in his head. (He is an able student.) and the reasons he, and we, need to give at each stage for full credit in an exam.
- Angle ABC = 108 – Its an angle in a Pentagon
- Triangle ABC is isosceles (Two of its sides are sides of a regular pentagon)
- <ACB = 36 – Its one of the other two angles in triangle ABC so = (180-108)/2
- <BCD = 108 – Its another angle in the pentagon
- <ACD = 72 – Angle ACD – ACB
- The answer DCF = 18 because its = 90 (Angle ACF, in the square) – 72( Angle ACD).And that is showing our working, with reasons. I think talented students sometime leave the rest of us behind with their logic, but explaining what we are doing is an important skill!
Now you have a few clues on how to work out those angles missing in any exam question.
You can find a list of facts about angles that can be used in this sort of question here